今回は系統発生学を紹介していこうと思います。系統発生学とは平たく言うと生物の進化を取り扱う学問分野です。進化というのはDNAに発生した変異が広がった場合に起こる現象です。ですので、DNA配列を系統発生学の眼鏡を通してみることで誰も見ていない何億年も前の歴史を知ることができるのです。今回から数回に分けてこんな系統発生学を紹介しようと思います。
突然変異が進化を誘導する
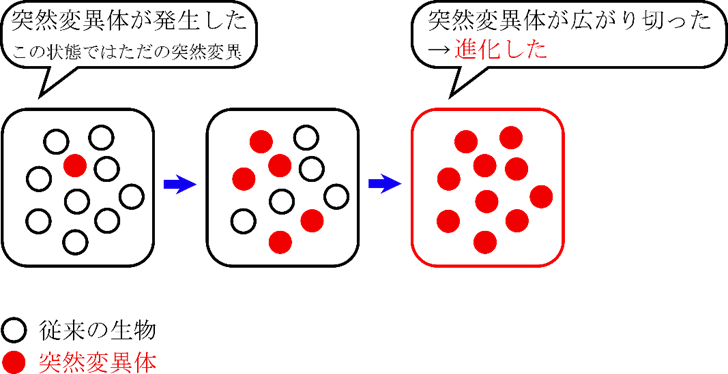
突然変異とは、DNA 上に変化が生じることをいいます。この変化はあくまで個体レベルでの変化であり、この時点では進化とはいいません。
さて、一度発生した変異はそのまま消えてしまう場合もあれば、その種の中に広がっていく場合もあります。発生した変異がその種に広がっていき、種全体に広がり切った場合、進化といいます。
進化に関する革新的な学説、中立説
進化に関する学説といえば、ダーウィンの進化論をイメージされる方は多いのではないでしょうか?しかし、現在の系統発生学では中立説という新たな学説が支持されています。ちなみにこの学説を提唱された先生は木村資生先生で、1968 年に提唱されています。この学説は分子情報から進化を推定するうえで極めて重要な学説です。そんな学説が日本人により提唱されているというのはなんだかうれしいですね。さて、この学説では変異を三つに分けて考えます。すなわち、有利な変異、不利な変異、中立な変異です。ここでそれぞれの発生頻度と進化に対する寄与の度合いを考えてみます。不利な変異や中立な変異に比べ有利な変異は圧倒的に少なく、進化の傾向を考える上では誤差の内になってしまいます。ですので思い切って有利な変異を無視します(無視できるほど少ないということです)。さらに、不利な変異についてはそのような変異を抱えた生物は生存できなくなるので消えてしまいます。したがってこの変異も進化に寄与しません。結果、進化に寄与する変異の大部分は中立な変異である、というのが中立説の主張です。
勘違いされる方がいるかもしれないので念のため言っておくと、中立な変異はアミノ酸置換が発生するものも含んでいます。タンパク質の機能に影響を及ぼさないような変異や構造に変化をもたらさないような変異はたとえアミノ酸が変化したとしても中立な変異といいます。
ダーウィンの自然淘汰説と中立説について議論してみます。間違ってはいけないのは中立説は自然淘汰説を否定していないということです。有利な変異が発生した場合は種内に広がるので進化に寄与しうるということは確かで、中立説でもこの点は否定していません。かつて、ダーウィンが進化論を研究した時代では、分子レベルで解析する術は開発されていませんでした。このような時代に用いられた手段は現存する生物の形態を比較して進化を議論する手段がとられていました(比較形態学といいます)。このような手段ではかなり大きな変異しか見つけることができないため、上記の三つの変異の内、有利な変異くらいしか検出することができなかったのです。ですので有利な変異が残っていった結果、進化につながったという自然淘汰説が提唱されるのは極めて自然なことだったと思います。ところが近年になって DNA 配列が決定できるようになると、有利でもなければ不利でもないような変異が圧倒的に多いということがわかってきました。このような変異を中立な変異と呼んでいます。中立説は近代的な解析技術が開発された結果、既存の自然淘汰説をアップデートしたととらえた方が正確な解釈ではないかと思います。
変異の発生頻度と進化速度は深く関連する
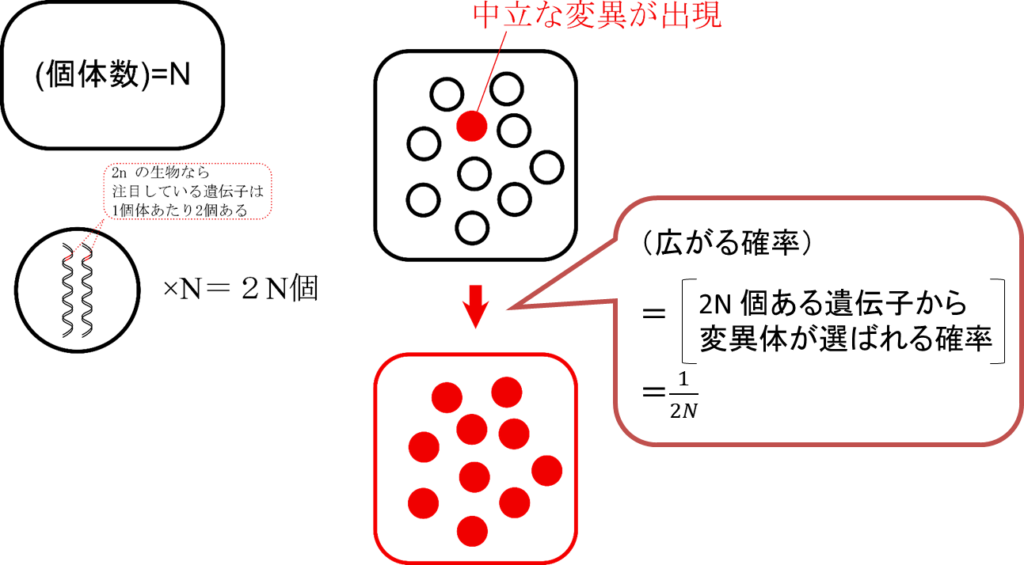
図2に図解しています。この図を見ながら説明していきましょう。まず、注目している種にN 匹の生物がいたとしましょう。ここではゲノムを2セット持つ生物(2n といいます。父方からの1セット、母方からの1セットで2セットです)を考えます。ゲノムというのはその生物が持っている遺伝子全部1セットと思ってください(念のため)。この場合、注目している遺伝子は1個体内に2個あります。したがって集団内には 2N 個の遺伝子があることになります。今、この中に1つの変異が出現したとします。すると、この変異が広がる確率は、この変異が 2N の中から選ばれる確率と考えると 1/(2N) となります(実はここで中立説が効いてきます。このような計算ができるのは 2N ある遺伝子がどれも等しく広がるチャンスをもっているからできる芸当です。もし起こった変異が有利だったりすると拡大する確率が変わってしまいますのでこのような単純な計算はできません)。
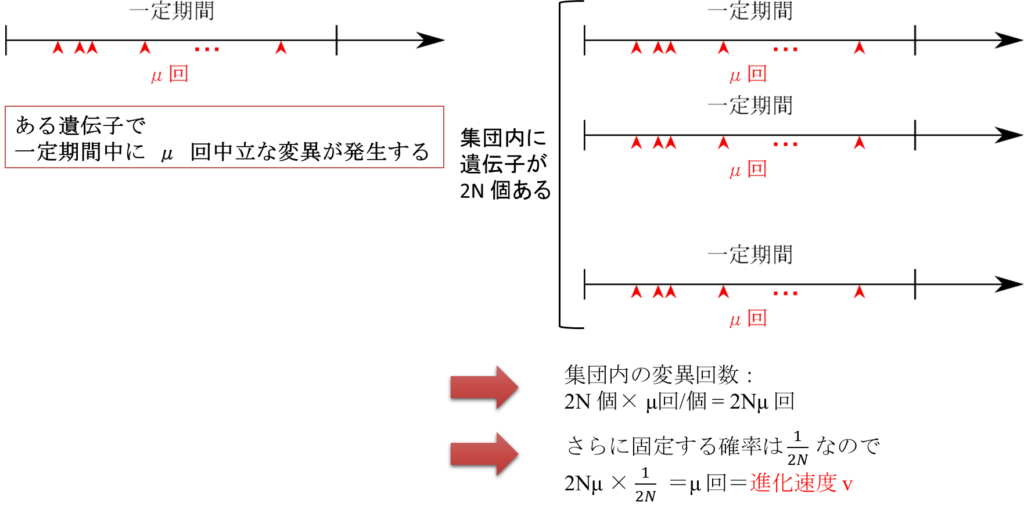
次に、ある遺伝子に発生する変異の頻度について時間軸に沿って考えてみます。一定期間内に一つの遺伝子で μ 回の中立な変異が発生するとします。集団全体でこの遺伝子は 2N 個あるので、一定期間内に集団全体で起こる変異の回数は 2Nμ 回となります。さらに、発生した変異が集団に広がり切る(集団に固定するといいます)確率は 1/(2N) なので、中立な変異が発生して集団に固定する頻度は 2Nμ × 1/(2N) = μ 回ということになります。さて、進化とは発生した変異が集団に固定することをいうのでした。その頻度が一定期間内に μ 回ということは進化が発生する頻度が一定期間内に μ 回ということです。したがって、進化する速度(変異が一定期間内に集団に固定する頻度)を v とすると v=μ となります。
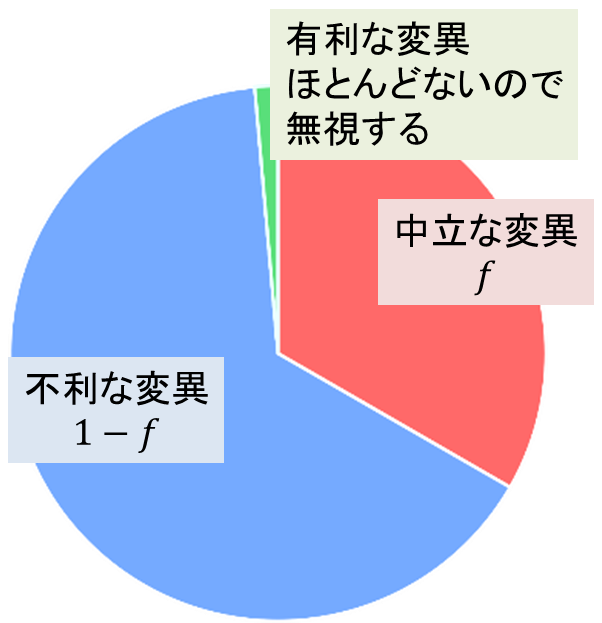
先ほどの μ は中立な変異が発生する頻度でした。次に、全突然変異の発生頻度を μT とします。そのうち中立な変異の発生する割合を f とすると、有利な変異はほとんどないので無視できると考えますので、不利な変異が発生する割合は中立な変異が発生する割合を差し引いた 1-f となります。さて、中立な変異が発生する頻度は fμT なので
(進化速度 v) = fμT となります。
なお、不利な変異が発生する割合 1-f は発生すると生物にとってうれしくない変異の割合です。このような変異はタンパク質の機能に影響を与えてしまう変異です。この点で突然変異は機能に影響与えないような制約を受けていると考えることができます。このことから 1-f のことを機能的制約といいます。
また、f≧0 であり、1-f≧0 でもあるので、0≦f≦1 なので、進化速度は f=1 の時に最大となります。
さて、今回は系統発生学の最も基本的な知見について紹介してみました。特に中立説は今後の数理モデルの基礎になっている重要な学説ですので、ぜひ理解していただけたら嬉しいです。今回はここまでにしようと思います。最後まで読んでいただいてありがとうございました。