解糖系はエネルギーを取り出すための代謝経路です。ですのでエネルギー収支はとても大切な観点です。(解糖系の各反応でなぜエネルギーが発生するのかは前回の記事「解糖系(glycolysis)によって糖からエネルギーを取り出しATP を生成する」を読んでください)で解説しました。今回は実際にどれくらいのエネルギーが発生し、ATP 産生に利用されるのか、また、ATPを利用する反応はどれくらいのエネルギーが要求されるのかといったことを数値的に理解してみましょう。
Contents
解糖系のエネルギー収支をギブスエネルギーに基づいて理解する
エネルギーを放出するか吸収するかによって反応が自発的に進むかを判断する指標になる
化学反応には自発的に進行してギブスエネルギーを放出するものとエネルギーを与えないと進行しないものがあります(ギブスエネルギーについては後述します。わからない方はそちらを読んでください)。反応の前後を比較した場合にギブスエネルギーが低下する方向に進む反応は自発的に進行します(これは高い位置にあるものが低い場所へ落ちるようなイメージです。この場合は位置エネルギーの高いほうから低いほうへ物体が移動します。このようにエネルギーの低いほうへ向かう現象は自発的に進行します)。この際余剰のエネルギーを放出します。このような過程は発エルゴン反応(exergonic reaction)といいます。一方でギブスエネルギーが増加する方向に進む反応はエネルギーを加えない限り進行しません(低い位置にある物体は持ち上げて移動させない限り高い位置には移動しませんね。位置エネルギーの低いものは持ち上げることでエネルギーを与えてあげない限り位置エネルギーの高い状態には移行しません)。このような過程は吸エルゴン反応(endergonic reaction)といいます。なお、ギブスエネルギーは系にエネルギーを与える方向をプラスにとります。したがってギブスエネルギー差がプラスの場合、吸エルゴン反応、マイナスの場合、発エルゴン反応ということになります。ここら辺はそういうルールにしましょうということですので覚えてください。
解糖系の反応はエネルギーの観点から四つに分類される
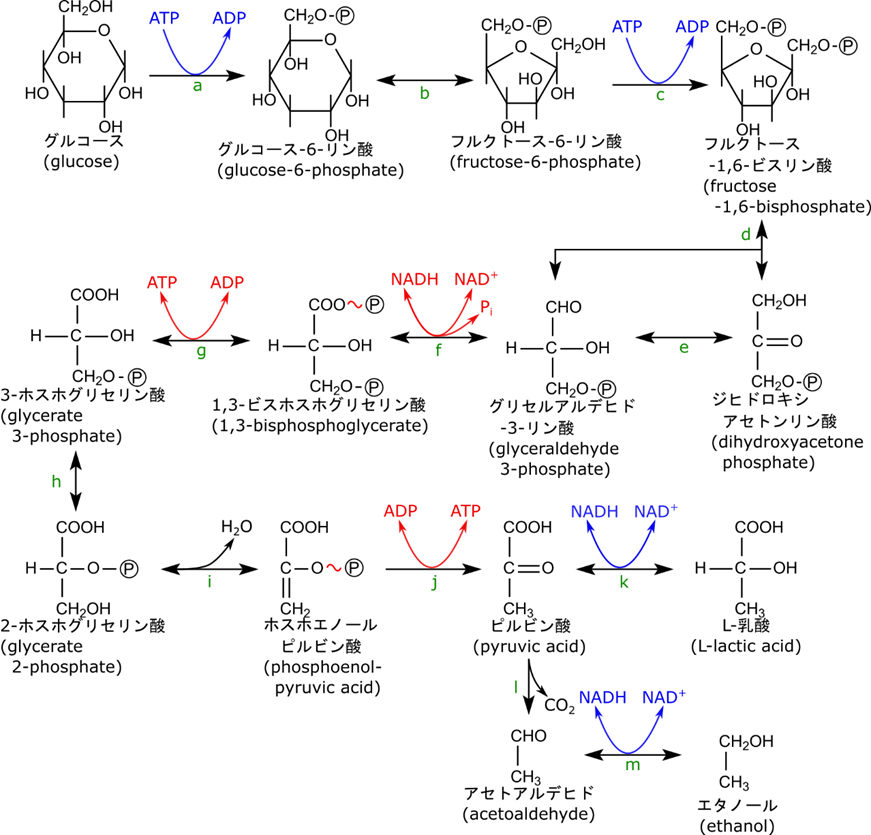
解糖系の反応も発エルゴン反応、吸エルゴン反応に分類することができます。各反応のギブスエネルギー変化を表1に示しました。表1の a ~ j は図0の a ~ j に対応しています。図0と表1を見比べながら使ってください。表1ではΔG゜’と記載しています。これは標準生理状態(圧力 1 atm, 温度 25℃, pH=7.0)でのギブスエネルギー変化を示しています。ややこしく見えますが、ギブスエネルギーは圧力、温度、pH に左右されるためこれらの値を一定にしておかないと比較ができません。ですので、ギブスエネルギーを考える場合にはこれらの数値をあらかじめ決めておく必要があります。そこで生物の体内でよくある数値を標準生理状態として規定しているというわけです。さて、解糖系の反応では吸エルゴン反応は反応 a, b, c, d, f, h が相当します。一方で発エルゴン反応は反応 e, g, i, j が相当します。吸エルゴン反応に注目してみましょう。吸エルゴン反応では 0.4 ~ 1.5 kcal/mol の比較的小さい吸エルゴン反応(反応 b, f, h)と、3.3 ~ 5.5 kcal/mol の大きい吸エルゴン反応(a, c, d)があります。一方で発エルゴン反応には -0.7 ~ -1.8 kcal/mol の比較的小さい発エルゴン反応(e, i)と -11.4 ~ 13.4 kcal/mol の大きい発エルゴン反応(反応 g, j)に分けられます。次からはこれら四つの分類についてそれぞれを見ていきましょう。
小さい吸エルゴン反応は吸エルゴン反応でも ATP を消費することなく反応が進む
小さい吸エルゴン反応は反応 b, f, h が相当します。ここで各反応の平衡定数 K’ を考えてみましょう。平衡定数 K’ は以下の式で求めることが可能です。
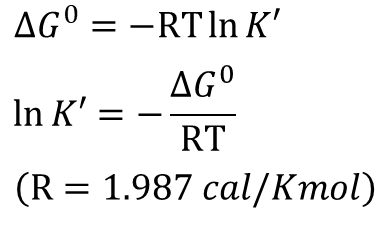
この数式を利用して、各反応の平衡係数を求めてみましょう。
- 反応 b:K’ = 0.51
- 反応 f:K’ =0.08
- 反応 h:K’ =0.17
平衡定数からおおよその反応物と生成物の存在比を算出することができます。例えば反応 b では平衡定数の定義から以下の式が成り立ちます。
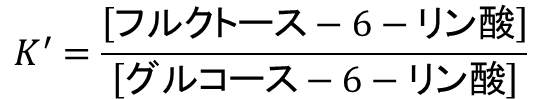
今、平衡定数が 0.51 ですので、グルコース-6-リン酸:フルクトース-6-リン酸のモル比はおよそ 2:1 になることがわかりますね(わかりにくければ [グルコース-6-リン酸] =2, [フルクトース-6-リン酸] = 1を代入してみてください。0.5 になって平衡定数 K’ に近い値になりますね)。反応 f、反応 h についても平衡は左に傾いていますが(反応物が多めですが)、生成物がその先の反応に使用されて濃度が低下していけば平衡を保つために反応物が生成物に変換されます。この過程が連続的に起こるため、反応自体は進みます。このように、小さい吸エルゴン反応では、吸エルゴン反応であっても平衡が成り立っているので生成物が減少するという条件の下では進行します。
大きい吸エルゴン反応では反応を進めるのに ATP を消費する
次のお話は大きい吸エルゴン反応に分類される反応 a, c, d についてです。反応 a と c についてはギブスエネルギー変化量が +3.3 kcal/mol と +3.9 kcal/mol とかなり大きな吸エルゴン反応です。そのため自発的には進行しない反応です。ですので、ATP を消費します。ATP が ADP に変換される反応はギブスエネルギー変化量が -7.3 kcal/mol の反応です。ですので、ATP の消費を込みでエネルギー収支を考えると、反応 a と c でそれぞれ、-4.0 kcal/mol、-3.4 kcal/mol となり、自発的に進行する反応になります。つまり、この反応では不足するエネルギーを ATP を消費して補っています。このため、反応 a と c は不可逆反応になっています。
反応 d では少し事情が異なります。この反応はギブスエネルギー変化量が +5.5 kcal/mol とかなり大きな吸エルゴン反応でありながら、ATP は消費されません。この反応の平衡定数 K’ を算出してみましょう。
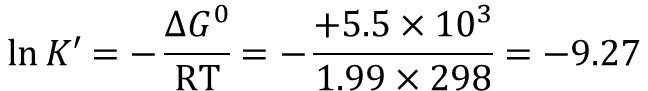
したがって K’=0.942×10-4≒1×10-4 です。さて、この平衡定数を使って平衡を考えてみます。
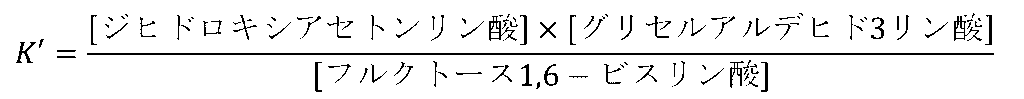
今仮に、フルクトース-1,6-リン酸濃度(反応物)を1 mol/L とすると、生成物は 10-2 mol/L になります(ジヒドロキシアセトンリン酸とグリセルアルデヒド3リン酸の濃度は一致として計算してみてください)。つまり反応物と生成物のモル比は 100:1 にもなってしまいます。ところが、反応物の濃度を10-3 ~ 10-4 mol/L まで低下させてみると反応物と生成物のモル比は 3.3 ~ 1:1 にまで低下します。さて、生理的な条件を考えた場合、反応物の濃度が 1 mol/L というのは異常に高い濃度になります。むしろ 10-3 ~ 10-4 mol/L という濃度の方が自然です。ですので実は生理的な条件下では反応 d は平衡を形成し、生成物が減少する状態では反応が進行するということになります。ですのでこの反応では ATP を消費しません。
小さい発エルゴン反応は可逆的であるが自発的に進む
小さい発エルゴン反応は反応 e, i です(ギブスエネルギー変化量はそれぞれ -1.8 kcal/mol と -0.7 kcal/mol)。この反応は発エルゴン反応であることからもともと自発的に進行する反応です。ただし、反応 e, i はいずれも平衡が成り立ちます。
大きい発エルゴン反応はエネルギー生成ステップ
大きい発エルゴン反応は反応 g と j です。これらの反応の(ATP を無視した場合の)ギブスエネルギー変化量は -11.8 kcal/mol と -13.4 kcal/mol です。ここで重要になる数値は -7.3 kcal/mol です。この数値は ADP をリン酸化して ATP にするのに要するエネルギーに相当します。反応 g と j のギブスエネルギー変化量は -7.3 kcal/mol を上回っていますね。したがって、得られたエネルギーをつかって ADP をATP に変換することができます。ADP → ATP の反応を込みでエネルギーを再計算してみると、反応 g と j のギブスエネルギー変化量はそれぞれ -4.5 kcal/mol と -6.1 kcal/mol となります。この場合でもこれらの反応は自発的に進行可能です。したがって大きい発エルゴン反応は解糖系のエネルギー生産過程とみなせますね。
ギブスエネルギーの観点から見る解糖系 まとめ
これまでいろいろと解説をしてきましたが、その内容をここで大雑把にまとめようと思います(覚えておくべき内容はこの内容で十分かと思います。上述の説明はこの内容を理解する助けとして理解してもらえたらうれしいです)。大きい発エルゴン反応は反応 g と j で、ATP の生産ステップになります。このステップでは大きなエネルギーが放出されるので、このエネルギーを利用して ADP が ATP に変換されます。大きい吸エルゴン反応は反応 a、c、d で、a、c では ATP を消費します。ただし、反応 d では例外的に ATP の消費はありません。それでも反応が進むのは前述したとおりです。そのほかの反応は小さい発エルゴン反応又は小さい吸エルゴン反応に分類されますが、これらの反応はいずれも可逆的な反応です。ところで、反応 a、c(大きい吸エルゴン反応の内 d 以外)と反応 j(大きい発エルゴン反応)の三つの反応は不可逆的です。実はこの三つの反応は制御において重要となりますので覚えておいてください。

ΔG゜’:標準生理状態(1atm, 25℃, pH=7.0)ギブスエネルギー変化
() 内はATP(ADP)の変化込で算出した数値
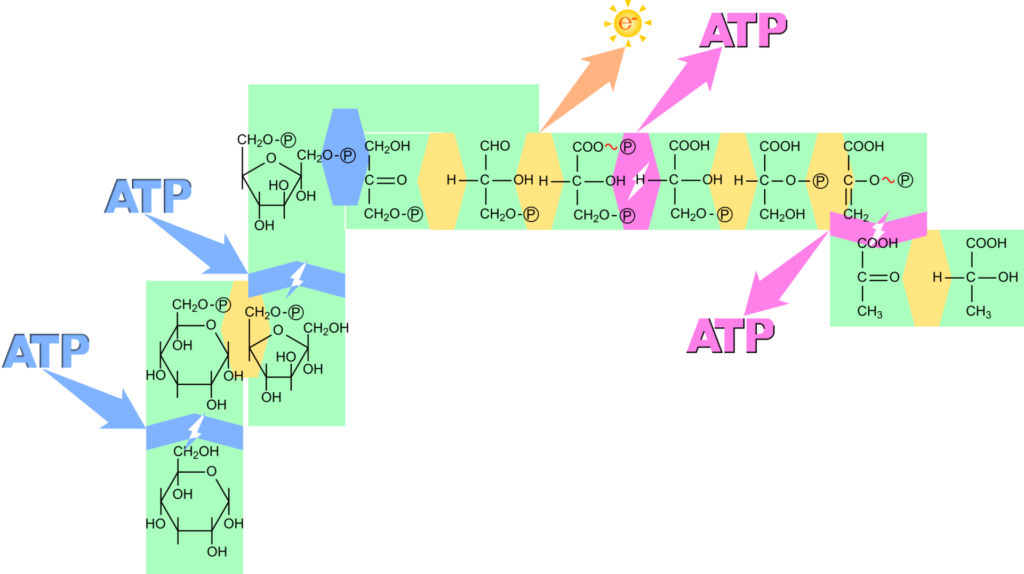
以上の内容を図でまとめてみましょう。この図では可逆反応を横配置、不可逆反応は縦配置で配置しています。大きい吸エルゴン反応は青矢印で、大きい発エルゴン反応は赤矢印で表しています。黄色は小さい吸エルゴン反応または小さい発エルゴン反応です。大雑把なイメージをつかんでくださいね。
ギブスエネルギーとは何を意味するのか?
ギブスエネルギーという言葉を多用してきましたが、ギブスエネルギーとは何でしょうか?ギブスエネルギーはギブスの自由エネルギーとも呼ばれます。こう聞いて何が自由なの?と疑問に思った方もいらっしゃることでしょう。ここではギブスエネルギーについて簡単に説明しようと思います(導出など詳細は熱力学を勉強してみてください)。
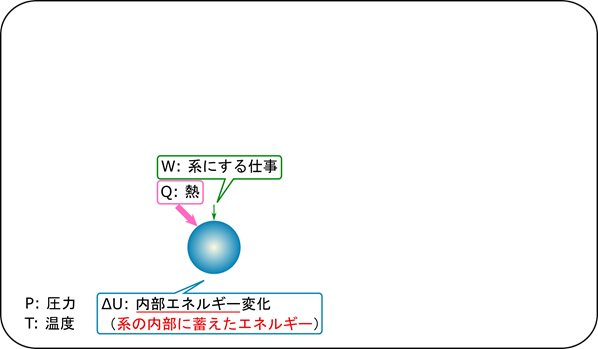
熱力学を考える場合には前提条件が大切になります。前提条件がないとどういう変化を取り扱うかの想定ができないためです。ギブスエネルギーを考える状況は大きな部屋の中にあるオープンな系です(上図)。この状況は実験室の中で化学反応をする場合に似ています。化学反応を起こしているビーカーなどはオープンなのでビーカー内の圧力と実験室の圧力は一致しますよね。また、大きな実験室の温度にとってビーカーの温度変化は微々たるものなのですぐに平衡化されてしまうため、反応の前後で一定します。このような温度と圧力が系の内外で同じでかつ一定している場合を前提としている場合を考えます。
ここで今回出てくる用語について簡単に解説します。各文字の前についている Δ は変化を意味します。今回は圧力(P)と温度(T)は一定なので変化しません(なのでΔはつきません)。また、系の内外で一致しているのでどちらについても圧力は P ですし、温度は T です。内部エネルギー(U)は系(今回はビーカーの内部ですね)が蓄えるエネルギーを意味します。このエネルギーが反応の前後で異なるとそこに仕事をしたり熱を加えないと反応が進まなかったり、余剰分が仕事になって出てきたりするわけです。熱はエネルギーではないのですが、与えることでエネルギーを増加させたり余剰のエネルギーが熱になってでてきたりします。そういう意味では熱はエネルギーに似ています。今回の場合は系の外と系の圧力と温度は一定で変化しないと仮定していますので、その点だけ注意してください。次にエントロピー(S)について確認しましょう。エントロピーの増加量 ΔS は
ΔS≧∫dQ/T
で表されます。Q は熱を表しますが、熱は分子の乱雑さ(バラバラ度合い)を増加させる量と解釈できます。一方で T は現在の系の乱雑さを表します。つまりエントロピーは乱雑さの増加量を現在の乱雑さでスケールした値と解釈できます。不等号になっているは熱の加え方によって乱雑さの増加量が変わるからです。熱を極めてゆっくり加えていった場合(系の分子が一様な状態を保ったまま熱を加えていった場合)、等号が成立します。そうではないような過程では乱雑さの増加量はより大きくなります。最後に仕事(W)について説明します。仕事というのは、物体に力を加えたとき、加えた方向に物体が移動した距離と力の掛け算で定義されます。重要なのは移動した方向と力を加えた方向が一致していなければいけません。熱力学で考慮する仕事は様々なものがありますが、特に膨張で発生する仕事(便宜上、膨張仕事といいますね)と膨張以外で行われる仕事(便宜上、非膨張仕事といいます)に分けて考えるとわかりやすいです。というのは系から仕事(あるいはエネルギー)を取り出すことを考えた場合は非膨張仕事がその最大値になるからです。膨張仕事は利用できません。以上が今回使用する用語の説明です。以降はギブスエネルギーの解説に戻りますね。
さて、上の図で示す状況でギブスエネルギーは
ΔG=ΔU+PΔV-TΔS
で定義されます。さらに、この反応が自発的に進む場合は
ΔG=ΔU+PΔV-TΔS≦0
という関係が成り立ちます。
ここでギブスエネルギーの意味について考えていきましょう。ギブスエネルギーのマイナス倍は系から取り出せる仕事の最大値という意味があります。ある過程が行われた場合、発生したエネルギーは内部エネルギーに変換されたり、熱になったり膨張仕事になってしまいます。これらのエネルギーや仕事は系から仕事を取り出して利用したいと考えた場合には自由にできないエネルギーということになります。逆に言うとこれらを差し引いた分のエネルギーが私たちが自由に使うことのできるエネルギーの最大値(というのはロスが発生することもあるためです)ということになります。この自由にできるエネルギーの最大値に相当するのがギブスエネルギーのマイナス倍ということになります。このことからギブスの自由エネルギーの意味が分かりますね。ここで出てくる ”自由” の意味は私たちが自由にできるエネルギー(の最大値)という意味なのです。もちろん相当うまくすれば非膨張仕事すべてを利用できますが、実際にはここからロスが発生します。ですので最大値ということになります。さて、解糖系では化学反応に伴って発生するエネルギーを使って ATP を産生していましたね。このエネルギーも当然上述の自由にできるエネルギーから利用しています。
ところで、ギブスエネルギーの定義式に注目てし下さい。ギブスエネルギーを規定するパラメータの中に圧力(P)や温度(T)が入ってますよね。これがギブスエネルギーの議論をする場合に圧力と温度を規定しないといけない理由です。ギブスエネルギーは環境要因として圧力や温度の影響を受けます。また、pH は分子の状態(例えば電離状態など)に影響を与えます。こういった分子の形態は内部エネルギーに影響を及ぼします。ということは上の式では ΔU に影響するということですね。ですので pH も重要なファクターということになります。ですのでこれまでの議論では圧力、温度、pH の三つを規定してから議論しています。この点は注意してください。なお、先ほども解説しましたが、ΔG゜’は標準生理状態(圧力 1 atm, 温度 25℃, pH=7.0)を意味していて、生物体内でよくある環境を採用しています。
解糖系から得られる ATP 収支は好気的か嫌気的かで大きく異なる
解糖系で得られるエネルギーを ATP で換算すると 2ATP になる
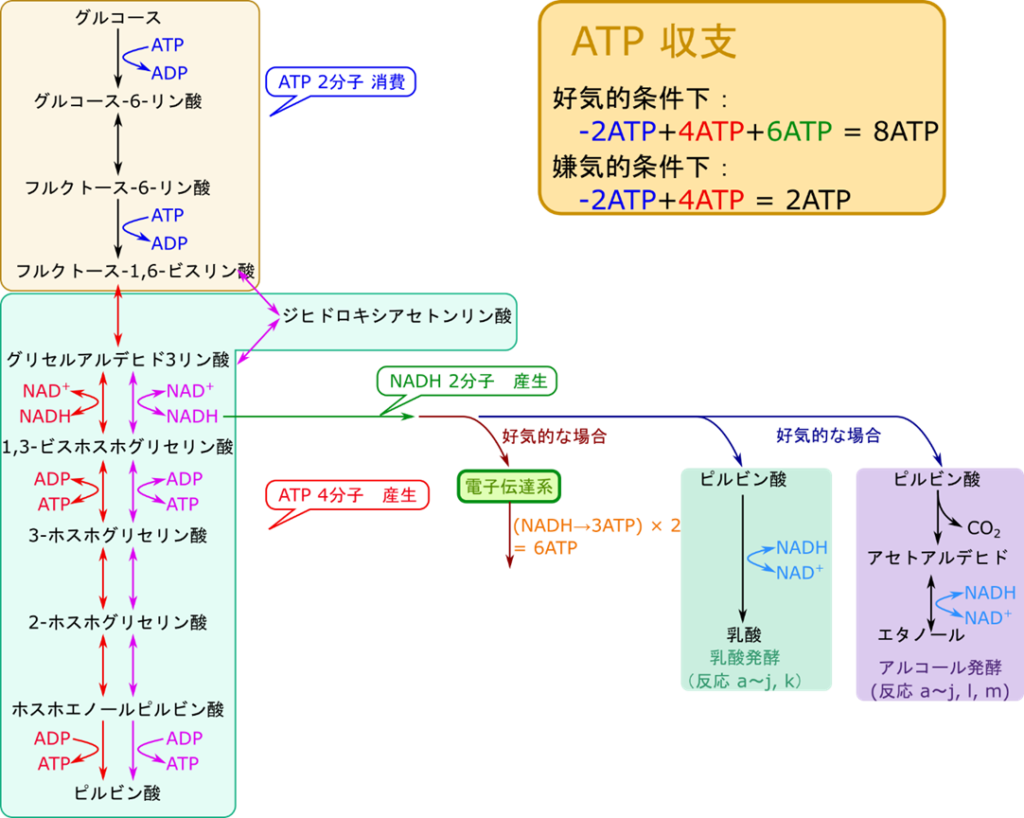
解糖系では ATP を消費するステップが 2 つと ATP を産生するステップが 2 つ存在します。一見 ATP 収支が±0 のように思われますよね。でも、実際にはフルクトース-1,6-ビスリン酸の開裂段階で炭素数 3 のジヒドロキシアセトンリン酸とグリセルアルデヒド3リン酸に開裂しますが、ジヒドロキシアセトンリン酸はグリセルアルデヒド3リン酸に異性化します。そのため、グルコース 1 分子から出発した場合、グリセルアルデヒド3リン酸以降の反応は 2 分子になることを意味します。イメージとしては図2の通りになります。黒矢印までは 1 分子の反応ですね。ところがフルクトース-1,6-ビスリン酸以降は赤矢印の経路とピンクの矢印の経路に分岐します。ただしこの二つの矢印はグリセルアルデヒド3リン酸で合流していますので結果的にはグリセルアルデヒド3リン酸以降の反応が 2 分子ずつが反応することになります。すると ATP の収支は 2 ATP × 2 – 2 ATP = 2 ATP となります。ちゃんと ATP 収支はプラスになりました。
NADH の代謝は好気的か嫌気的かによって異なる
解糖系では NAD+ が NADH に変換されます。この NADH はどこかで NAD+ に変換されなければ再利用ができません。好気的な条件では NADH は電子伝達系(electron transport system)で酸化され、NAD+ に変換されます。電子伝達系では NADH から電子を引き抜いて最終的には酸素に渡します。この場合、NADH 1 分子当たり 3 分子の ATP が産生されます。解糖系ではグルコース 1 分子当たり 2 分子の NADH が産生されますから、NADH の代謝に伴って 6 分子の ATP が産生されることになります。ですので、これらの効果も考慮したうえで ATP 収支を考えてみると 8 ATP が産生されることになります。この経路は酸素を要求しますので好気的でなければなりません。
一方で嫌気的な条件では電子伝達系に NADH を渡すことはできません。そこでピルビン酸やアセトアルデヒドに電子を引き渡して NAD+ に変換されます。この場合はピルビン酸は還元されて乳酸に変換されますし(ケトンの還元)、アセトアルデヒドは還元されてエタノールに変換されます(アルデヒドの還元)。このような過程は醗酵と呼ばれます。この場合は ATP の産生はないため ATP の収支は 2ATP となります。
このように解糖系から得られる ATP 収支は好気的か嫌気的かによって大きく異なります。なお、私たちヒトでは通常好気的な条件で解糖系は機能します。ですのでかなり高効率で ATP 産生をすることが可能です。しかし、急激な運動をした場合は一時的に嫌気的な状態に置かれます。ですので、解糖系は嫌気的な条件で動くことになり乳酸が産生されることになります。これはエネルギーを早く作り出す必要があるため NADH を電子伝達系に渡して処理する暇がないためです。
今回は解糖系のエネルギー収支について議論してきました。ちょっと物理の知識も入りますので難しく感じるかもしれませんが、今後化学反応を考える上では大事な知見になりますのでイメージをしっかりつかんでいただけると今後の学習に大変役立つと思います。それでは今回はここまで。次回は解糖系の制御などについて解説していきます。お疲れ様でした。
参考文献
- 島原健三 (1991). 概説 生物化学. 三共出版. pp. 151-162
- Jeremy M. Berg, John L. Tymoczko, Gregory J. Gatto Jr., Lubert Stryer著、入村達郎、岡山博人、清水孝雄、中野徹訳 (2018). ストライヤー生化学 第8版. 東京化学同人. pp. 416-442
- John McMurry著、伊東椒、児玉三明訳 (2000). マクマリー有機化学 第4版. 東京化学同人. pp. 365-367, 546-551
- Paula Y. Bruice 著、大船泰史、香月勗、西郷和彦、富岡清訳 (2016). ブルース有機化学概説 第3版. 化学同人. pp. 678-729
- 石原顕光著 (2019). しっかり学ぶ化学熱力学 エントロピーはなぜ増えるのか(電子書籍版).裳華房.
関連記事
糖鎖の基本について
糖鎖の化学反応について
糖鎖の表記方法・三文字表記について
オリゴ糖・多糖について
解糖系について
- 解糖系(glycolysis)によって糖からエネルギーを取り出しATP を生成する
- 解糖系の各反応をエネルギー的観点から読み解く
- 解糖系で利用される糖はグルコースに限らない
- 解糖系の制御は三つの律速酵素に対する調節で行われる
TCA サイクルについて