双性イオンとアミノ酸の特性：物理化学的性質を深掘りします

　アミノ酸にはカルボキシル基とアミノ基があります。これらの置換基は pH によって負に帯電したり、正に帯電したりします。このためアミノ酸は pH に応じて実に様々な挙動を見せてくれます。この特性はアミノ酸によって構成されるタンパク質の多種多様な性質を生み出す源泉にもなっています。この記事ではアミノ酸が形成する双性イオンに注目して解説していこうと思います。

Contents

1 双性イオンとして存在するアミノ酸
2 参考文献

双性イオンとして存在するアミノ酸

アミノ酸の物理化学的性質は双性イオンに起因する

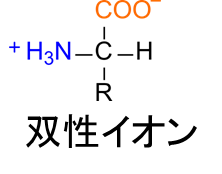
　アミノ酸は、溶液中では図１のようなカルボキシル基（-COOH）のプロトンがアミノ基（-NH₂）に転位した双性イオン（１分子内に正電荷と負電荷の両方を持つイオン）の形で存在しています。この性質のため、隣接するアミノ酸同士を強く引き付けあうので密度が高くなります。また、分子同士の引力が強くなるために融点が高くなる傾向があります。

溶液中のアミノ酸のカルボキシル基はプロトンを失い負電荷をもつ置換基になる。一方でアミノ基はプロトンを獲得して正電荷を持つ置換基になる。この結果、アミノ酸は双性イオンとして存在することになる — 図１．双性イオンとしてのアミノ酸

アミノ酸水溶液での挙動（中性アミノ酸）

　中性アミノ酸は以下の通りです。

アラニン
バリン
ロイシン
イソロイシン
メチオニン
フェニルアラニン
トリプトファン
プロリン
グリシン
セリン
トレオニン
アスパラギン
グルタミン

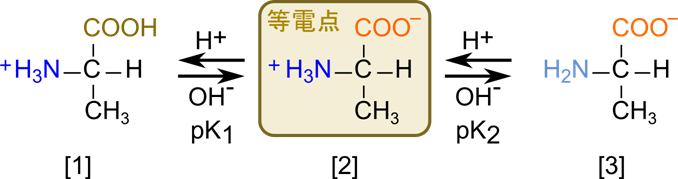
　中性アミノ酸の水溶液中の挙動をアラニンを例に考えてみましょう。アラニンは溶液にすると図２の [2] のような双性イオンになります。この分子種は負電荷をもつ置換基（-COO^–）と正電荷を持つアミノ基（-NH₃⁺）を一つずつ持っているため、電荷が打ち消しあって電気的に中性となります。ここに酸あるいは塩基を添加するとどうなるでしょうか？

[2] に酸を添加すると、アラニンは陽イオンになる
1. [2] に酸を添加すると、カルボキシル基にプロトンが付加して -COOH となり、
  電荷が打ち消されます（図２の [1] の分子種）
2. アミノ基は正電荷、カルボキシル基は電荷をもたないので、
  分子全体としては陽イオンになります。
[2] に塩基を添加すると、アラニンは陰イオンになります
1. [2] に塩基を添加すると、アミノ基からプロトンが脱離して -NH₂ となり、
  電荷が打ち消されます（図２の [3] の分子種）
2. カルボキシル基は負電荷、アミノ基は電荷をもたないので、
  分子全体としては陰イオンになります

アラニンは溶解すると双性イオンの形態になる。そこに酸を添加すると、カルボキシル基がプロトンを獲得して、分子全体は陽イオンとなる。一方で塩基を添加するとアミノ基からプロトンが脱離して、分子全体は陰イオンになる。 — 図２．酸あるいは塩基を添加した場合のアラニンの変化

　これらの反応はいずれも平衡をなしています。[1] と [2] の平衡を考えてみましょう。この反応は以下の通りです。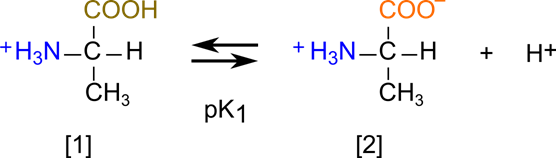

この時の酸解離定数を K₁ とすると K₁ は以下のように定義されます。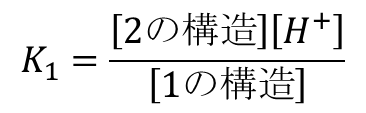

なお、以下のように pK₁ を定義します。

一般に、アミノ酸の特性を表す場合には K₁ ではなく pK₁ を使用します。
この時、[1] の構造がプロトンを放出するので（Brønsted-Lawry の）酸であり、[2] は共役塩基となります。一方で逆の反応を考えた場合 [2] の構造がプロトンを受け取りますので塩基となり、[1] は共役酸となります（Brønsted-Lawry の酸・塩基についてはこちらをご覧ください）。ここで、Henderson-Hasselbalch の式を利用すると、pH が算出できます。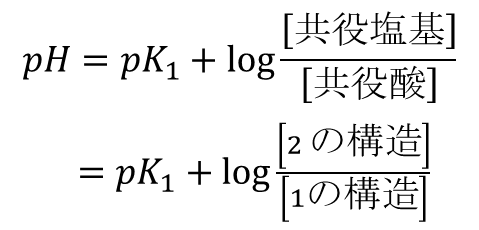

今、pH が pK₁ の時を考えます。

ですので、pH=pK₁ の時 [1] と [2] が同濃度で存在します。
同様に、[2] と [3] の平衡を考えると、以下のような反応になります。

したがって、K₂ は以下のように定義されます。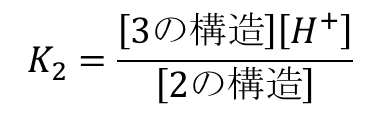

なお、以下のように pK₁ を定義します。

K₁ と同様に、アミノ酸の特性を表す場合には pK₂ を使用します。
この時、[2] の構造がプロトンを放出するので（Brønsted-Lawry の）酸であり、[3] は共役塩基となります。一方で逆の反応を考えた場合 [3] の構造がプロトンを受け取りますので塩基となり、[2] は共役酸となります（Brønsted-Lawry の酸と塩基は相対的に定義されるので、同じ物質でも場合によっては酸にも塩基にもなりえることに注意してください）。Henderson-Hasselbalch の式を利用すると、pH が算出できます。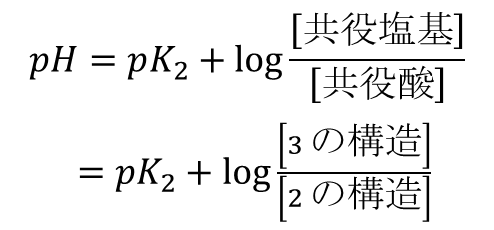

今、pH が pK₂ の時を考えます。

ですので、pH=pK₂ の時 [2] と [3] が同濃度で存在します。
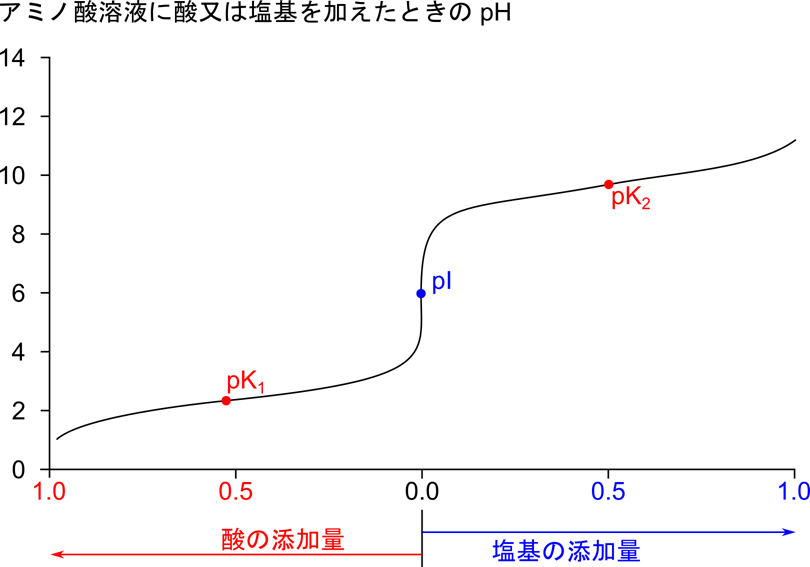
　ところで、アラニン溶液の pH を変動させていくと図２の [2] のような構造がほとんどを占める状態になります。このようなときの pH を等電点（isoelectric point）といいます。このポイントでは電荷が打ち消されてアラニンは電気的に中性になります。中性アミノ酸の場合、pI は pK₁ と pK₂ の間にあり、以下の式で算出されます。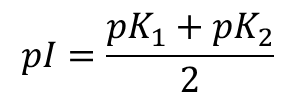

なお、アラニンでは pI = 6.00 となります。
　アラニン溶液の酸あるいは塩基による滴定曲線を見てみましょう。pH が pK₁ や pK₂ と等しい点では滴定曲線の傾きが緩やかになっています。このことは pH が pK₁ や pK₂ 付近にある時、アラニン溶液が緩衝作用を有していることを意味しています。

アラニンの滴定曲線では、pK1、pK2 の２点で緩衝作用を示す。pI は pK1、pK2 の中点に存在しています。 — 図３．アラニンの滴定曲線

アミノ酸水溶液での挙動（酸性アミノ酸など）

　この項目に当てはまるアミノ酸は以下の通りです。システインとチロシンは酸性アミノ酸ではありませんが、システインではチオール（-SH）が -S^– に、チロシンでは -OH が -O^– に変換されるため、酸性アミノ酸のように挙動します。

アスパラギン酸
グルタミン酸
システイン
チロシン
（フェノールのように電離した方が共鳴構造をとるのでプロトンを放出しやすい）

　酸性アミノ酸の場合、中性アミノ酸とは異なり側鎖にカルボキシル基を持っています。そのため、平衡は図４のように３段階になります（なお、システインとチロシンも上述の通りプロトンを放出するので、酸性アミノ酸のように挙動します）。[2] の構造をとる場合、電荷は打ち消されて、分子全体として電荷をもたなくなります。なお、この時の側鎖のカルボキシル基は -COOH となります。

[2] に酸を添加すると、アスパラギン酸は陽イオンになる
1. [2] に酸を添加すると、カルボキシル基がプロトンを受け取ります。
2. 電荷をもつ置換基は -NH₃⁺ のみなので、
  分子種は陽イオンになります（アスパラギン酸＝Aとして、A⁺）。
[2] に塩基を添加するとと、アスパラギン酸は陰イオンになる
1. [2] に酸を添加すると、側鎖の -COOH のプロトンを放出します。
2. 電荷をもつ置換基は -COO^– 二つと -NH₃⁺ があるので、
  分子種は一価の陰イオンになります（A^–）。
[3] に塩基を添加するとと、アスパラギン酸は二価の陰イオンになる
1. [3] に塩基をさらに添加するとと、アミノ基がプロトンを放出します。
2. 電荷をもつ置換基は -COO^– 二つがあるので、
  分子種は二価の陰イオン（A^2-）となります。

それぞれの酸解離定数を以下のように定義します。

[1] ⇆ [2] の酸解離定数を pK₁
[2] ⇆ [3] の酸解離定数を pK₂
[3] ⇆ [4] の酸解離定数を pK₃

なお、アスパラギン酸の場合、pK₁ = 1.88、pK₂ = 3.65、pK₃ = 9.60 です。等電点は分子種のもつ電荷がなくなる点ですので、[2] の分子種がほとんどをしめる点になります。等電点の求め方は、等電点を挟んで両側の pK 値を足して２で割ると求まります。したがって以下のように求めることができます。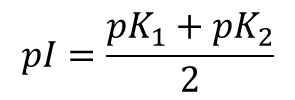

なお、アスパラギン酸の場合は　pI = 2.77 となります。

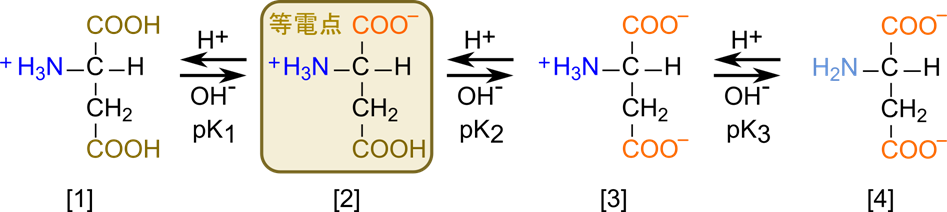
　滴定曲線を確認してみましょう。アスパラギン酸では pK₁、pK₂、pK₃ の３点で緩衝作用を示します。このことは、これらの点で敵的曲線の傾きが緩くなっていることから確認できますね。さらに、pI は pK₁ と pK₂ の間に存在しています。

アスパラギン酸の滴定曲線では、pK1、pK2、pK3 の３点で緩衝作用を示す。pI は pK1、pK2 の中点に存在しています。 — 図５．アスパラギン酸の滴定曲線

アミノ酸水溶液での挙動（塩基性アミノ酸）

　塩基性アミノ酸は以下の通りです。

リシン
アルギニン
ヒスチジン

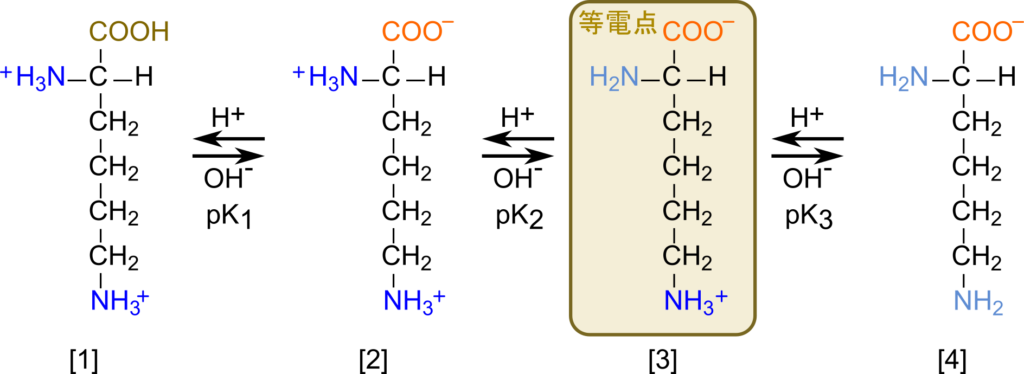
　塩基性アミノ酸の場合、側鎖にアミノ基を持っています。そのため、平衡は図６のように３段階になります。[3] の構造をとる場合、電荷は打ち消されて、分子全体として電荷をもたなくなります。中性や酸性のアミノ酸のように [2] ではないので注意してください。なお、この時の側鎖のアミノ基は -NH₃⁺ となります。

[3] に酸を添加すると、リシンは一価の陽イオンになる
- [3] に酸を添加すると、α アミノ基がプロトンを受け取ります。
- 電荷をもつ置換基は -COO^– と -NH₃⁺ 二つがあるので、
  分子種は分子は一価の陽イオンになります（リシン＝Aとして、A⁺）。
[2] に酸を添加するとと、リシンは二価の陽イオンになる
- [2] に酸を添加すると、カルボキシル基がプロトンを受け取ります。
- 電荷をもつ置換基は -NH₃⁺ 二つがあるので、
  分子種は二価の陽イオンになります（A²⁺）。
[3] に塩基を添加するとと、リシンは陰イオンになる
- [3] に塩基をさらに添加するとと、アミノ基がプロトンを放出します。
- 電荷をもつ置換基は -COO^– があるので、
  分子種は陰イオン（A^–）となります。

それぞれの酸解離定数を以下のように定義します。

[1] ⇆ [2] の酸解離定数を pK₁
[2] ⇆ [3] の酸解離定数を pK₂
[3] ⇆ [4] の酸解離定数を pK₃

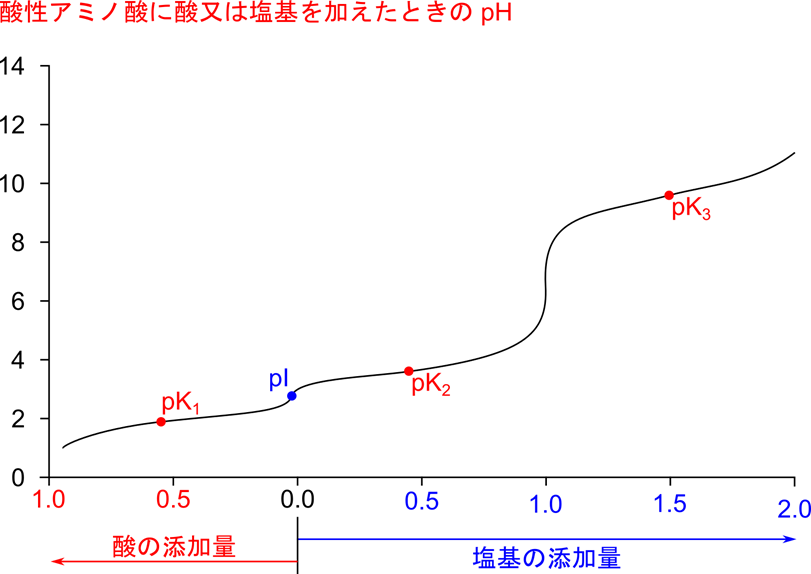
なお、リシンの場合、pK₁ = 2.18、pK₂ = 8.95、pK₃ = 10.53 です。等電点は分子種のもつ電荷がなくなる点ですので、[3] の分子種がほとんどをしめる点になります。等電点の求め方は、等電点を挟んで両側の pK 値を足して２で割ると求まります。したがって以下のように求めることができます。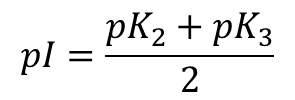

pI がどのポイントに来るかを理解するとわかると思いますが、 pK₂ と pK₃ を利用する点に注意してください。なお、リシンの場合は　pI = 9.74 となります。

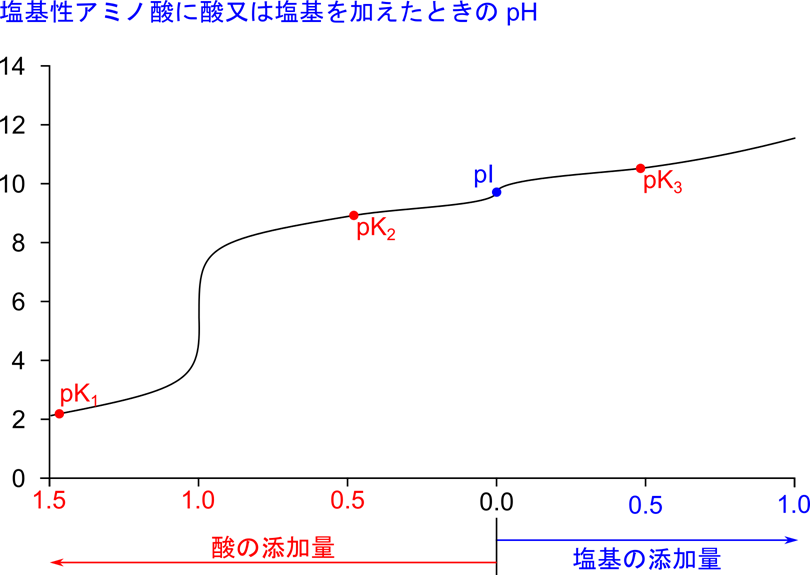
　滴定曲線を確認してみましょう。リシンでも pK₁、pK₂、pK₃ の３点で緩衝作用を示します。このことは、これらの点で敵的曲線の傾きが緩くなっていることから確認できますね。さらに、pI は pK₂ と pK₃ の間に存在しています。

リシンの滴定曲線では、pK1、pK2、pK3 の３点で緩衝作用を示す。pI は pK2、pK3 の中点に存在しています。 — 図７．リシンの滴定曲線

Henderson-Hasselbalch（ヘンダーソン・ハッセルバルヒ）の式について

　今回の解説で pH を算出しています。この時に利用している算出式を導出してみましょう。
　以下の平衡を考えます。
　HA + H₂O ⇆ H₃O^– + A^–
この時、平衡定数 K は以下のようになります。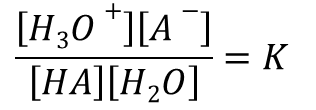

H₂O は酸に対して十分に多いと想定できますので、反応の前後で一定と考えられますので、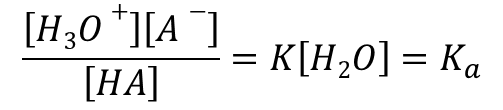
・・・（＊）
とみなせます。一方で、定義から pH と pKa は以下のように算出できます。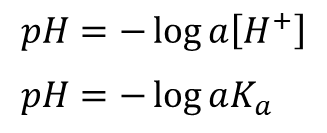

a[H⁺] や aK_a は活量と呼ばれる値です。水素イオン濃度など、粒子濃度が高いと各粒子がぶつかり合って自由度が制限されます。その結果、見かけの粒子の作用が制限されます（下図）。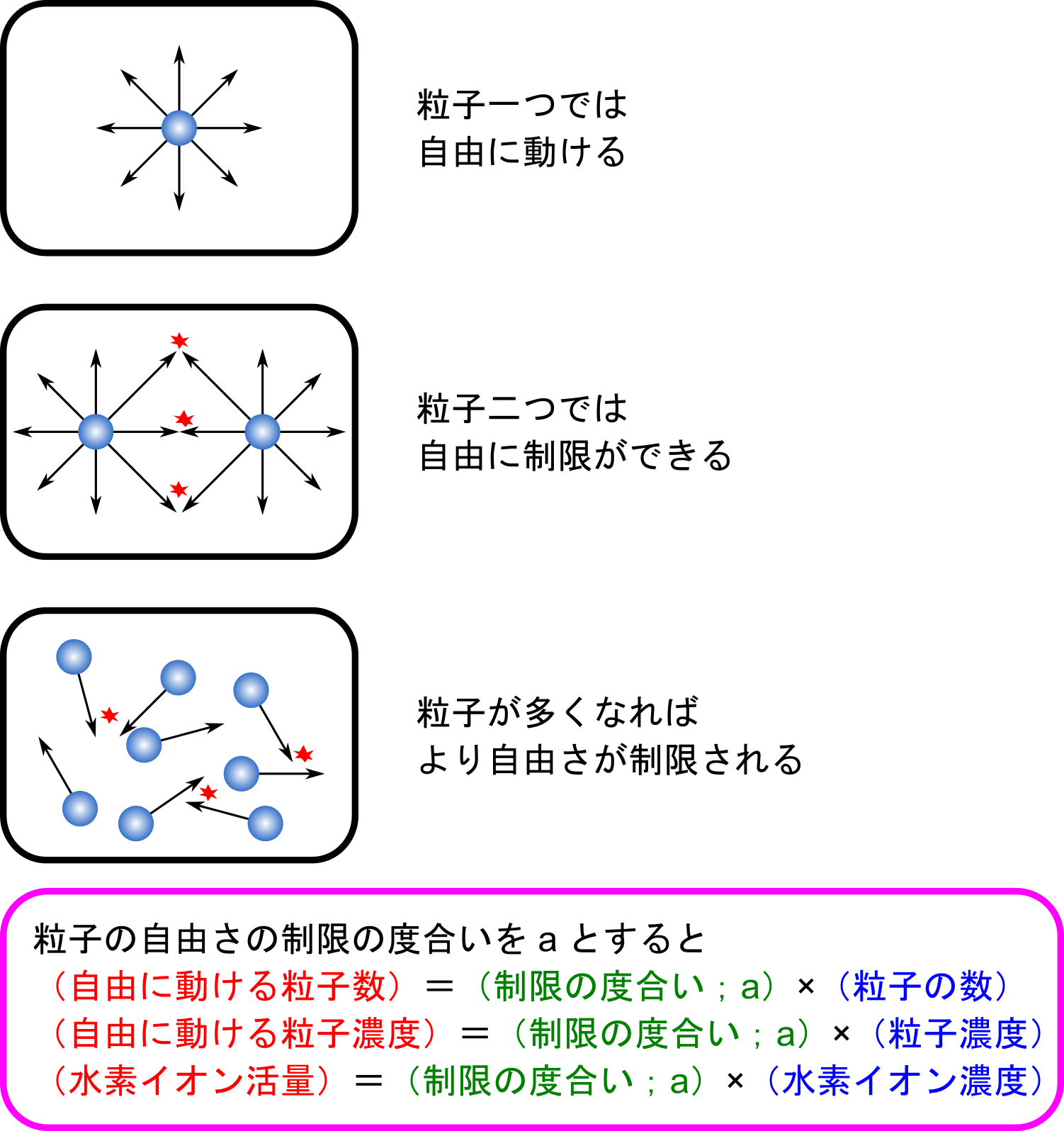

　この制限の度合いを考慮した実質的な濃度のことを活量といいます。ただし、この影響は粒子の濃度が十分に小さい場合には（粒子同士のぶつかり合いはほぼ起こらないので）無視することができます。ですので、[H⁺] や [H₃O⁺] と [A^–] が十分に小さい場合、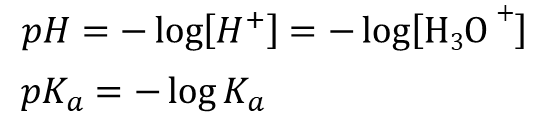

したがって（＊）から、以下の式が導けます。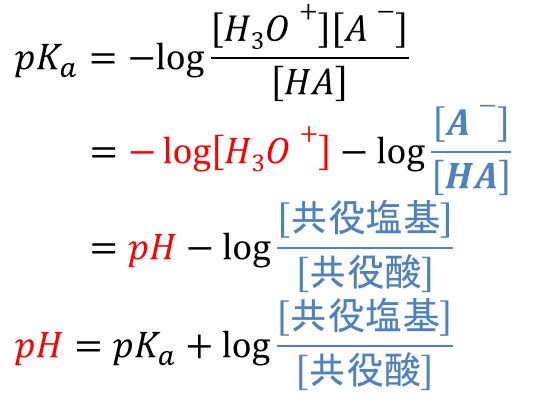

この式は、Henderson-Hasselbalch（ヘンダーソン・ハッセルバルヒ）の式と呼ばれており、pH を算出する際に利用することができます。