アロステリック酵素については以前の記事(こちら)で紹介しましたが、この酵素は Michaelis Menten の式に従いません。ですので、アロステリック酵素の化学速度論については異なるモデルで考察する必要があります。今回はアロステリック酵素に利用されるモデルについて紹介します。
Contents
化学速度論
アロステリック酵素は Michaelis-Menten の式に従わないので、これに変わるいくつかのモデルが提唱されています。ここではヒルプロット(Hill Plot)と協奏モデル(Concerted Model)を紹介します。これらのモデルはよくヘモグロビンの酸素との親和性を説明するために使用されます。ヘモグロビンは酵素ではありませんが、ヘモグロビンとアロステリック酵素は類似した点があります。アロステリック酵素が触媒する反応の速度はアロステリック酵素と基質の親和性の上昇・下降に影響されています。実はヘモグロビンは酸素が結合することで酸素との親和性が上昇する性質を持っており、この特性はホモトロピックなアロステリック効果と類似しています。ですので、ヘモグロビンと酸素の親和性を説明するモデルはアロステリック酵素と基質の親和性を説明するモデルとしても有用なのです。では、これらのモデルについて具体的に見ていきましょう。
ヒルプロット
Archibald Hill によって 1913 年に提唱されたモデルです。このモデルでは以下のような反応を考えます。![]()
この反応の解離定数Kd は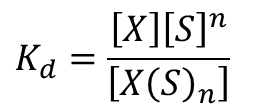 ・・・①
・・・①
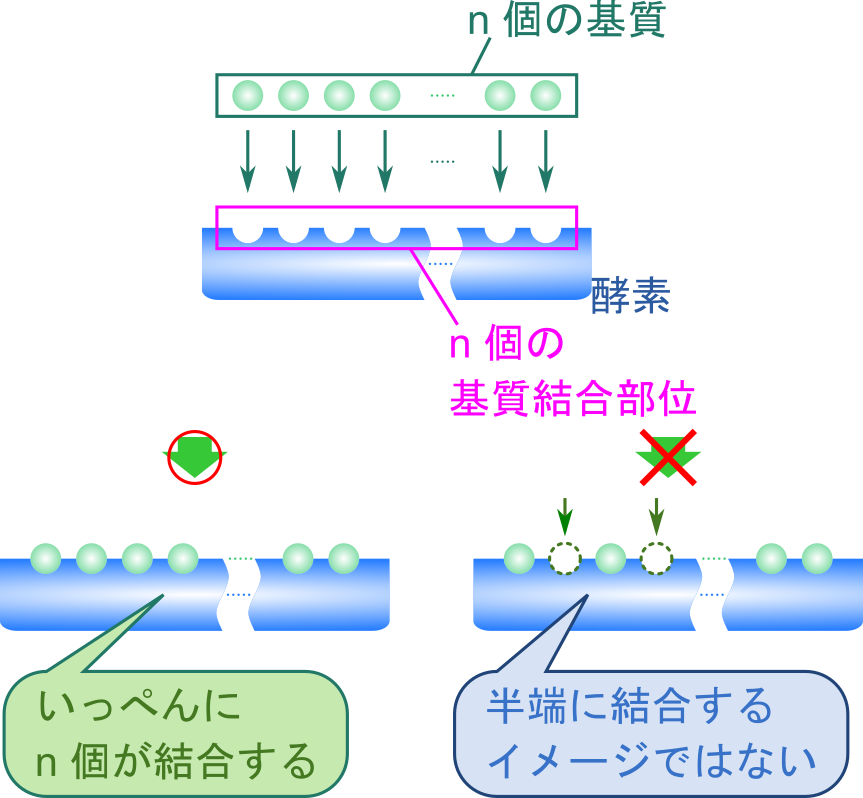
ここで、Hill プロットでは便宜上、n 個の基質が一段階で結合すると考えます。実際には常にいっぺんに n 個が結合するわけではありませんが、このように考えることで計算がかなり簡単になります。ここで、飽和度(fractional saturation of sites)を定義します。飽和度は全基質結合部位濃度に対する結合した基質濃度の比で表します(つまり基質で満たされている基質結合部位の割合です)。今回の場合、全基質結合部位濃度は n[X] + n[X(S)n] で、結合した基質濃度は n[X(S)n] ですので、飽和度 Y は以下の通りです。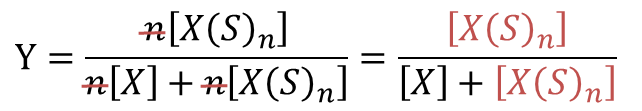 ・・・②
・・・②
①より、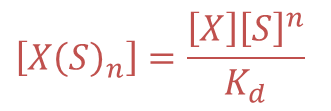
なので②に代入して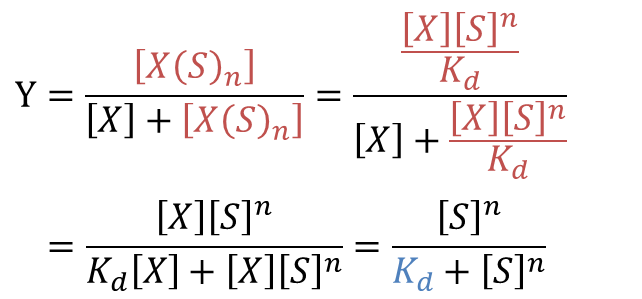 ・・・③
・・・③
酵素の50%が基質と結合したとき、基質と結合した酵素 X(S)n と基質と結合していない酵素 X の濃度は一致するので、
[X(S)n]=[X]
この時の基質濃度を S50 とすると①の式を利用して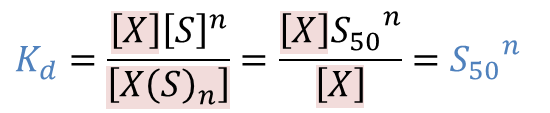
この関係を③に代入する
SとS50は異なる点に注意!!
S:基質濃度
→様々な値をとる変数
S50:酵素の50%が基質と結合したときの基質濃度
→酵素毎に特有の定数
混同しないように気を付けてください。
少し技巧的ですが、Y/(1-Y) をとります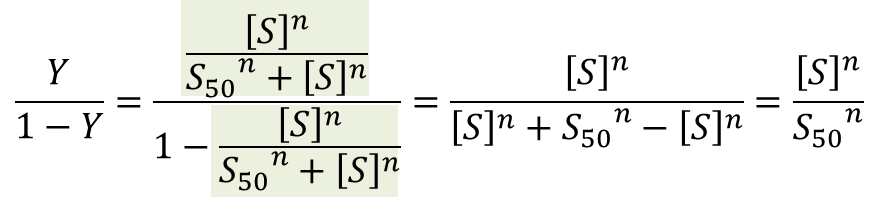
両辺の対数をとると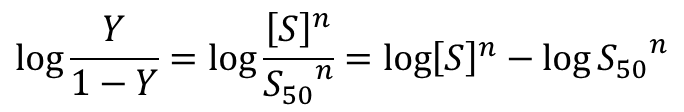
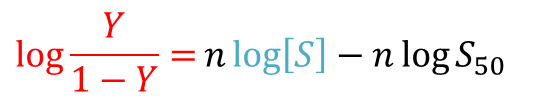
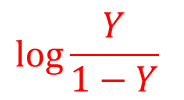 を y,
を y, ![]() を x とみなすと、
を x とみなすと、![]()
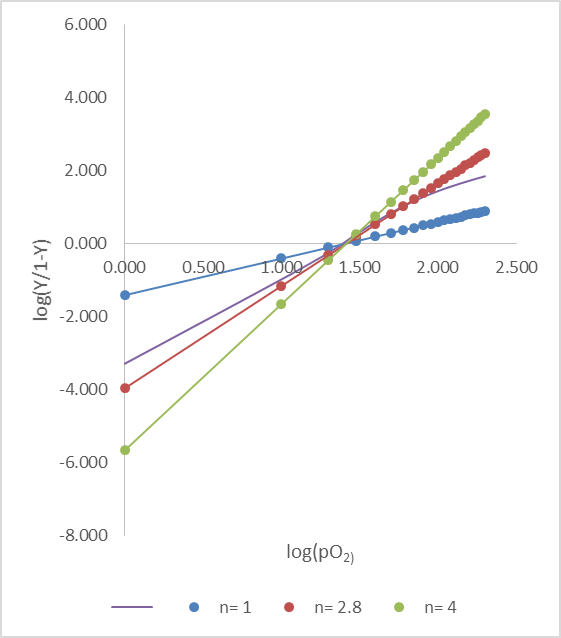
● n=1, ● n=2.8, ● n=4 としてプロットをとった。紫は実際に得た Hill プロット。n=2.8 の時、実際のプロットに最も近くなる。
この式は直線の式となっています。この時、n はヒル係数(Hill coefficient)と呼ばれ、基質の協同性の程度(基質の結合が他の基質の結合を促進する度合い)を示す指標となります。
このことから、基質濃度とY/(1-Y) の対数をプロットすると直線になることがわかります。この関係は非常にシンプルでわかりやすく、実際の関係を近似できるのですが、n 個の基質がいっぺんに酵素へ結合するという仮定のため、実際のプロットと比較すると少しずれる場合があります。この点を改善したモデルが次に紹介する協奏モデルです。
協奏モデル

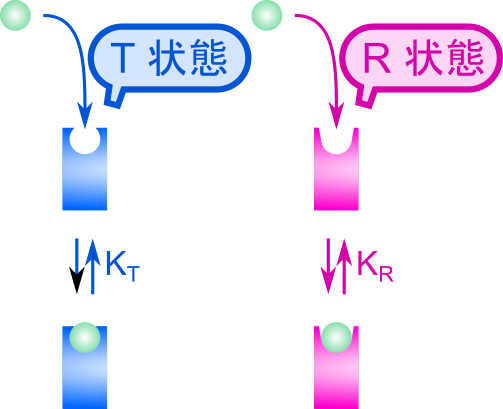
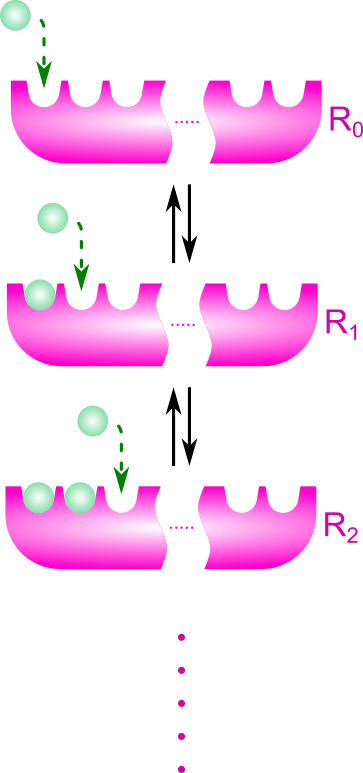
協奏モデルでは以下の前提条件を想定します。
- 基質結合部位が n 個ある
- 基質結合部位はT状態かR状態のいずれかをとる
- R(Relaxed)状態:基質との親和性大
- T(Tense)状態 :基質との親和性小
次に添え字の確認をします。
- Ri:i 個の基質が結合した R 状態の酵素
- Ti:i 個の基質が結合した T 状態の酵素
とします。また、Li を Ri と Ti の濃度比と定義します。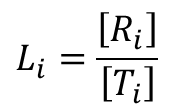
i = 0 の時、すなわち基質が結合していないときの L0 は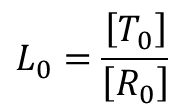 ・・・①
・・・①
R状態あるいはT状態の時の一つの部位当たりの解離定数をそれぞれ KR、KT とします。
この時、
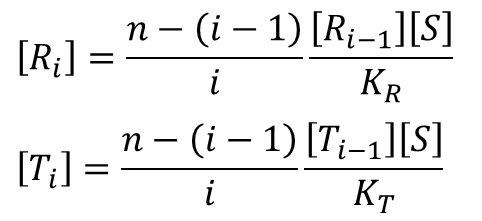
となります。この点について考えてみましょう。
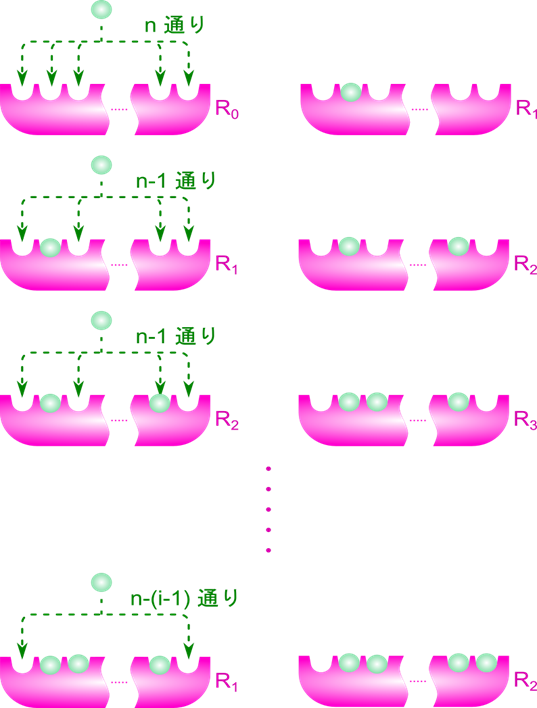
R0→R1 のときについて考えます。
KR はひとつの結合部位当たりの解離定数です。今、i 番目の結合部位に基質が一つ結合しているときの R 状態の酵素をRi1 とおくと、
となります。
ところで、R状態の酵素には n 個の結合部位があるので、Ri1 は n 通りが考えられます。このことから、 Ri1 の濃度は n 通りあるうちの一つと考えて R1 の 1/n と考えられます。したがって、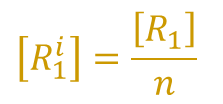
であり、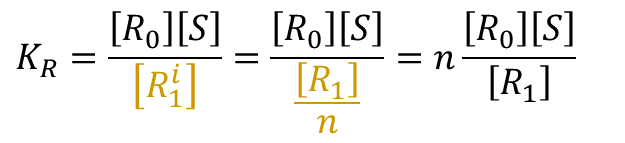
となります。
次に、R1→R2 のときについて考えます。
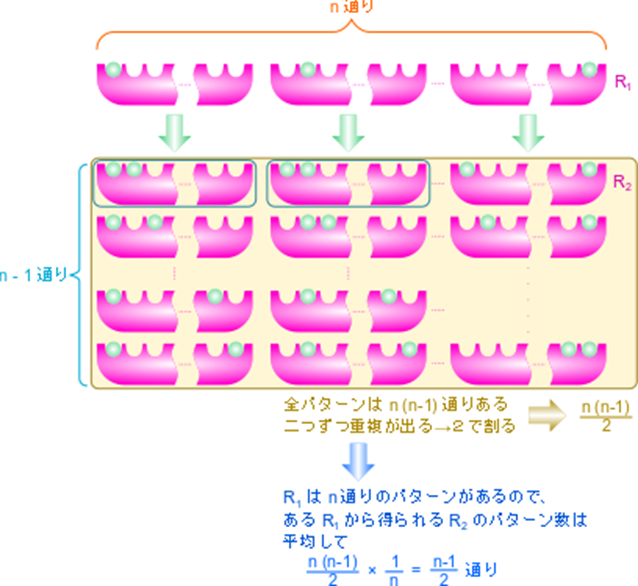
i 番目と j 番目の基質結合部位に基質が結合している R 状態の酵素を Ri,j2とします。Ri1 からできる Ri,j2 のパターンは n-1 通りです(基質結合部位の内一つはすでに結合しているので、j の取りうる値は n-1 通りです)。一方で、Ri1 の取り得る状態は n 通りありますので、Ri,j2 の取り得るすべての状態は n(n-1) 通りですが、Ri,j2 とRj,i2 は i 番目と j 番目の基質結合部位が基質と結合している点では同等であり、見分けがつきませんから、n(n-1) 通りという数え方をした場合、二通りずつ重複して数えていることなります。ですので、R2 の取り得る状態は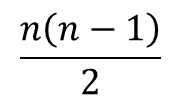 通りです。Ri1 は n 通りあるので、Ri1 からできる Ri,j2 取り得るパターンの期待値は
通りです。Ri1 は n 通りあるので、Ri1 からできる Ri,j2 取り得るパターンの期待値は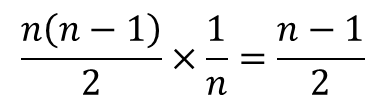
となります。したがって、この場合における Ri,j2 の濃度は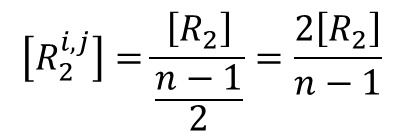
このことから、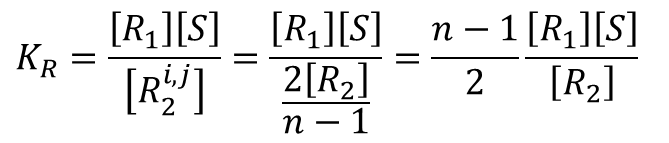
となります。このことから、結局 Ri1 から Ri,j2 ができるパターン数 (n-1) を、重複するパターン数( Ri1 → Ri,j2 と Rj1 → Rj,i2 が重複)で割った値 (n-1)/2 を [R1][S]/[R2] にかければよいことがわかります。
R2→R3 となるとき、同様に考えると、まず空いている基質結合部位は n-2 個ですから、もう一つ基質が結合して得られる R3 のパターン数は n-2 通りあります。ただし、異なる状態の R2 から同じ状態のR3 が得られるパターンは、結合している三つの基質から最後に結合する基質を選ぶパターンを考えればよいので、3通りとなります。したがって、この 3 通りは重複して数えていることになりますので 3 通りで割って、R2 から得られる R3 のパターンは 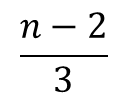 通りです。したがって、
通りです。したがって、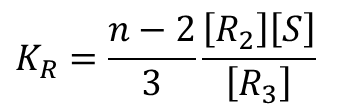
となります。
このように順次考えていくと、Ri-1→Ri となるとき、空いている基質結合部位は n-(i-1) 個ですから、基質が結合する可能性は n-(i-1) 通りあります。ただし、どの基質が i 番目かは考慮しないので、i 通りで割ると Ri-1 から得られる Ri のパターンの期待値がわかります。このことから、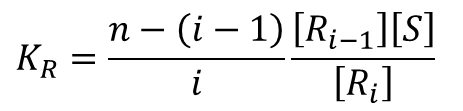
となることがわかります。
この式を変形すると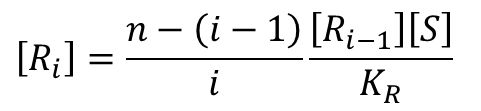
同じように考えると(RをTに変えてみてください。)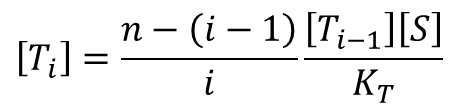
となります。
この関係を i=0 まで下げていくと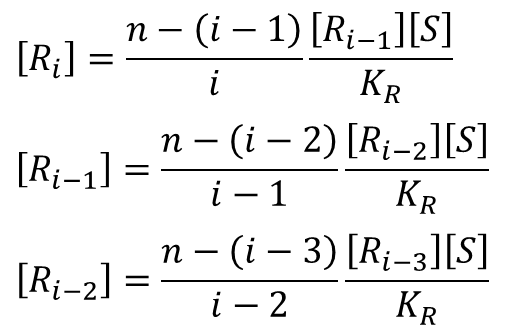
・・・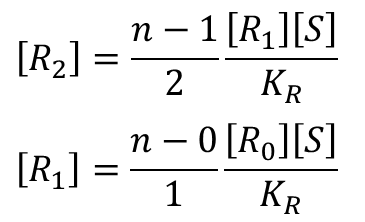
となります。これを[Ri] の式に代入していくと、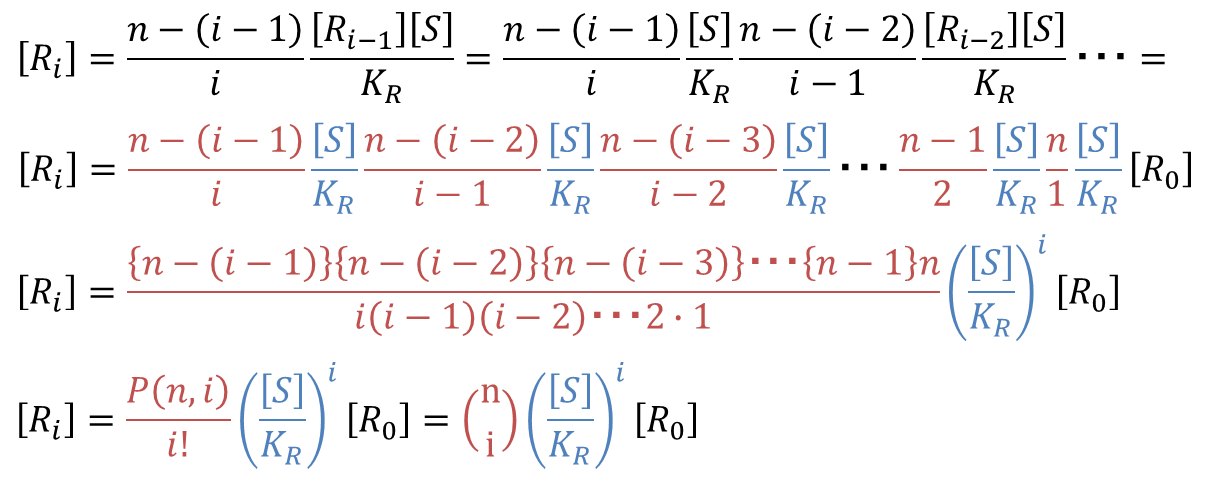
念のため記載方法を確認します。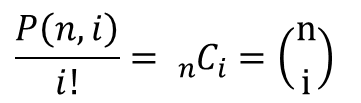 となり、組み合わせのことを意味します。
となり、組み合わせのことを意味します。
ここで導出された 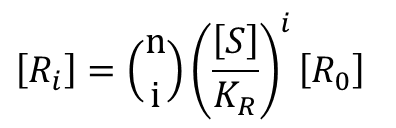 について考えってみましょう。
について考えってみましょう。
仮に基質は1 から順番に結合していくと仮定しましょう。この場合は結合する順番が決まっているので、R1、R2、・・・Ri はいずれも一種類しかありません。したがってこの場合に限っては以下のような関係が成り立ちます。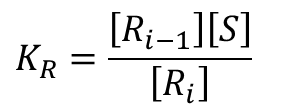
この式を変形すると、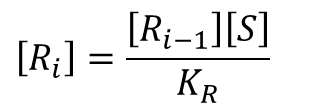
となります。この式利用すると、[Ri] の一般式が導けます。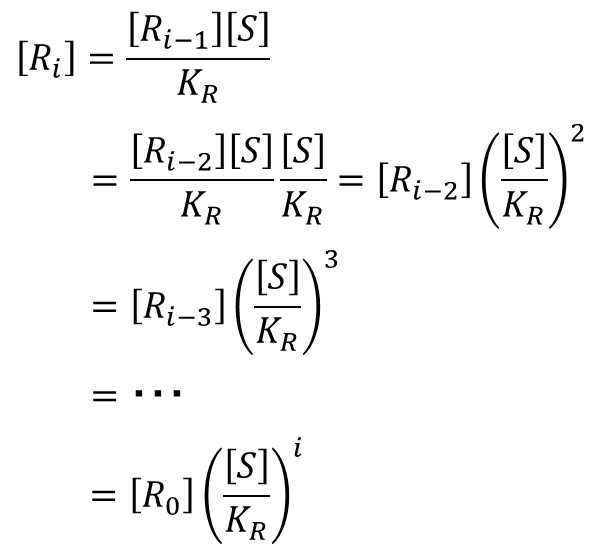
ところが、実際には基質は様々なパターンで結合します。i 個の基質が結合するパターンの数は n 個の基質結合部位から i 個の基質が結合した部位を選ぶ組み合わせですので、![]() 通りとなります。これまで考えてきた [Ri] はこのうち一パターンしか考えていませんので、実際の [Ri] は
通りとなります。これまで考えてきた [Ri] はこのうち一パターンしか考えていませんので、実際の [Ri] は![]() 通りをかけて
通りをかけて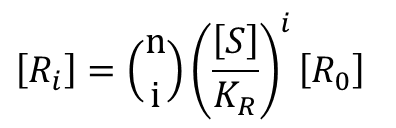
となり、結局同じ式が導出されました。
ところで、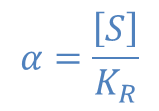 とおくと
とおくと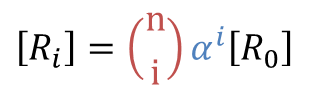 ・・・②
・・・②
同様に考えると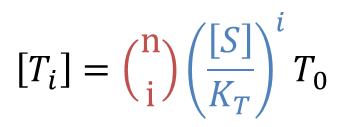
となります。ところで、①より![]()
また、 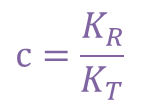 とおくと
とおくと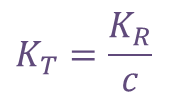 なので、
なので、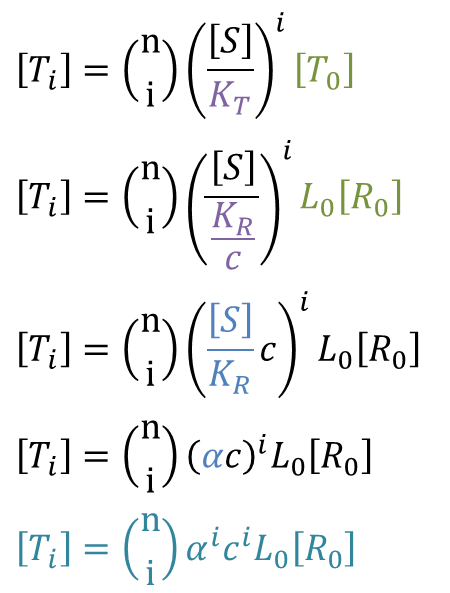 ・・・③
・・・③
今、i 個の基質が結合している酵素が R 状態から T 状態へ移行する反応を考えます。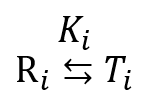
この Ki は以下のように計算できます。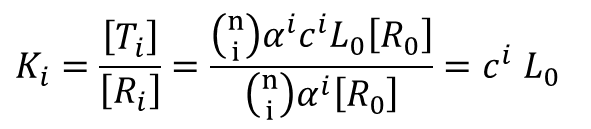
次に飽和度について考えましょう。
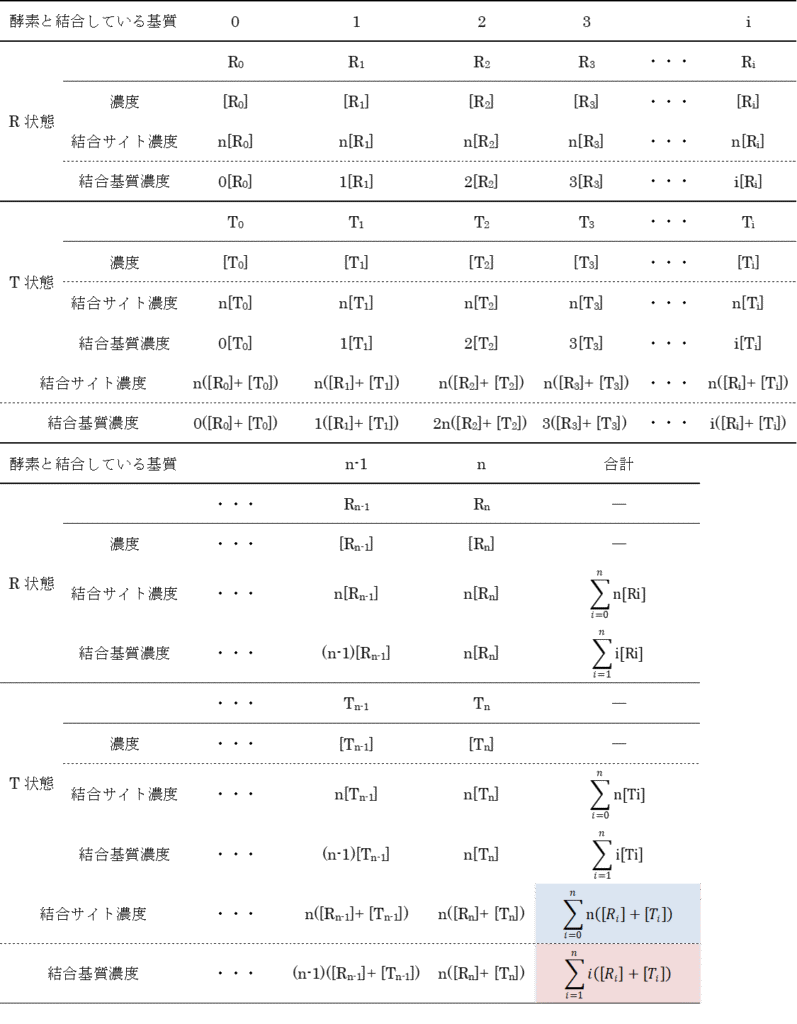
酵素一つが n 個の基質結合サイトを持っているので、全結合サイト濃度は以下の通りです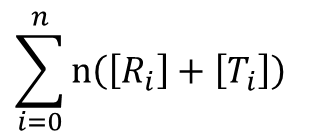
また、酵素に結合している基質濃度は以下の通りです。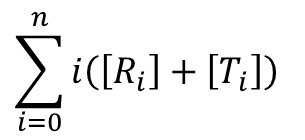
これらの式は以下の表を参考に考えてみてください。例えば、R2 に注目すると、R2 が持つ酵素結合部位は一分子当たり n 個ありますので、R2 状態の酵素結合部位の濃度は n[R2] となります。また、結合している基質数は 2 個ですから、R2 に結合している基質濃度は 2[R2] となります。このことを結合している基質数ごとにまとめたものが以下の表です。ところで、R 型の酵素と結合している基質の数は 0, 1, 2,・・・, i,・・・n-1, n ですので、基質結合部位濃度は nR0 + nR1 + nR2 + ・・・ + nRn となりますし、結合している基質濃度は 0R0 + 1R1 + 2R2 + ・・・ + nRn となります。T 状態についても同様に考えられますので、上記の式が得られます。
したがって飽和度Yは以下のようになります。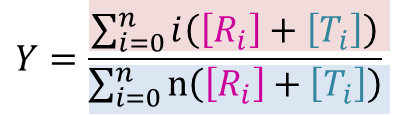
さらに、②③を代入すると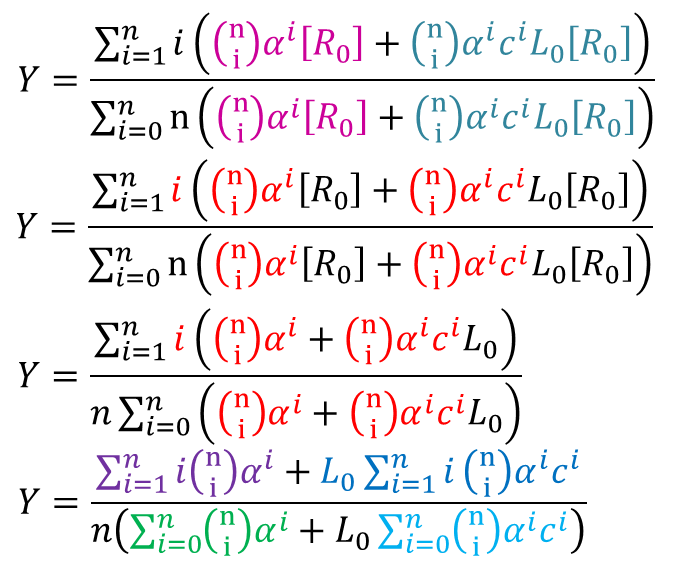 ・・・④
・・・④
(赤字は i を含む項を表しています。この項は定数項ではないので Σ の外に出すことはできません)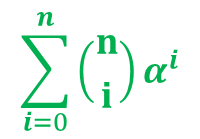 について考えましょう。
について考えましょう。
この式は以下のように二項定理を利用することでシンプルな形に変形できます。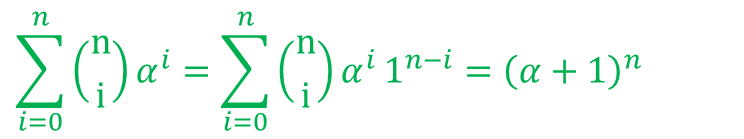 ・・・⑤
・・・⑤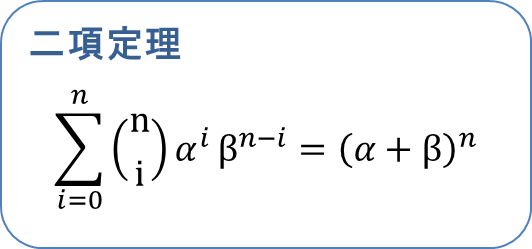
同様に(α を cα に置き換えると分子の第二項についても同様に変形できます)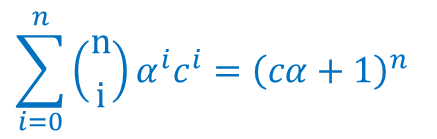 ・・・⑥
・・・⑥
次に、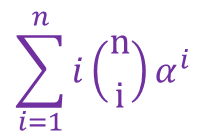 について考えましょう。この項は分子の第一項と似ていますが、最初に i がついているので少し工夫が必要そうですね。そこで以下のように変形してみましょう。
について考えましょう。この項は分子の第一項と似ていますが、最初に i がついているので少し工夫が必要そうですね。そこで以下のように変形してみましょう。 したがって
したがって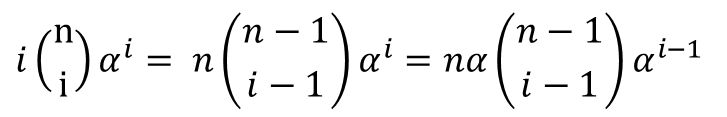
このことから、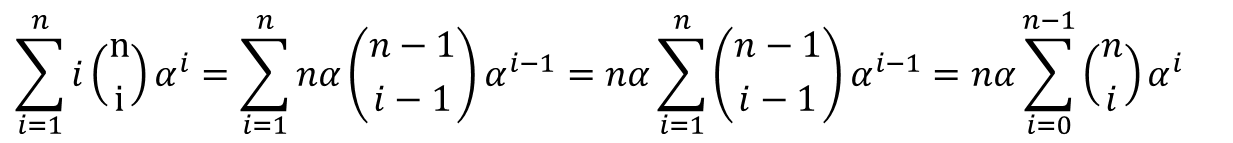
この変形では i が Σ の中で動く数字を表現しているにすぎない点に注意してください。i が 1~n の範囲をとるとき、i-1 は 0 ~ n-1 の範囲をとります。そこで、i-1 を i に置き換えて、この i が 0~n-1 の範囲をとるとすると同じことを意味します。このことを以下のような対応表で確認してみましょう。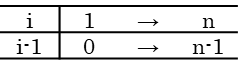
一応展開すると以下の通り。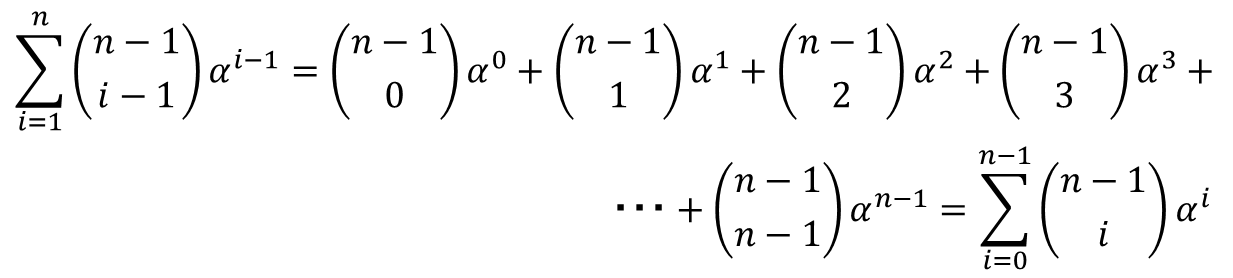
すると、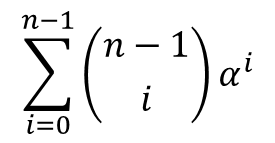 部分は⑤の導出と同じように考えると以下のように変形できることがわかります(n を n-1 に変えてみてください)。
部分は⑤の導出と同じように考えると以下のように変形できることがわかります(n を n-1 に変えてみてください)。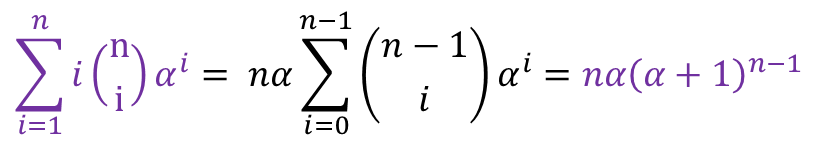 ・・・⑦
・・・⑦
同様に考えて分母の第二項を変形すると(α を cα に置き換える)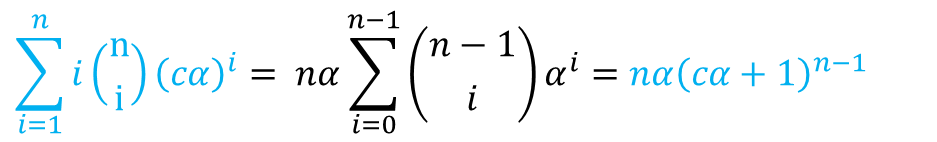 ・・・⑧
・・・⑧
④~⑧より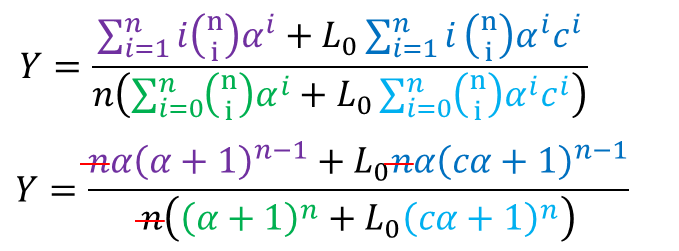
したがって、以下のような式が導出されました。この式は協奏モデルにおける基質濃度 [S] と飽和度 Y の関係を表す式となっています。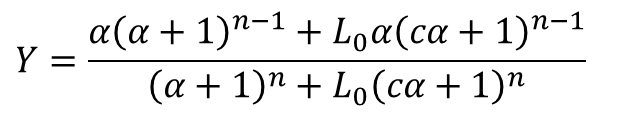
ただし、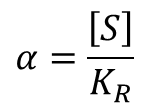 です。
です。
この式では、L0、c、KR、n がこの曲線を特徴づける数値です。なお、この関係式では α と Y が変数となります。したがって、協奏モデルを決定する段階では、適切な L0、c、KR、n を見つけ出すことがポイントになります。一方で、すでに適切な協奏モデルがわかっている場合には与えられた L0、c、KR、n を代入して挙動を予測するモデルとして利用します。
例えば、ヘモグロビンでは、L0=9000、c=0.014、KR=2.5 Torr として、n=4 とすると実態とよくフィットします。この時のグラフを以下に示しました。なお、ヘモグロビンの場合は酸素との親和性を考えていますので、酸素分圧として示していますが、これは状況に応じて基質濃度に置き換えて考えることもできます。さて、協奏モデルでは飽和度だけでなく、以下の式を利用することで酵素の各状態 T0~T4、R0~R4 の濃度比の推移も予測することが可能となります。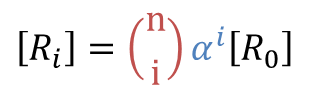
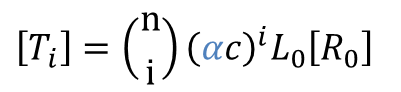
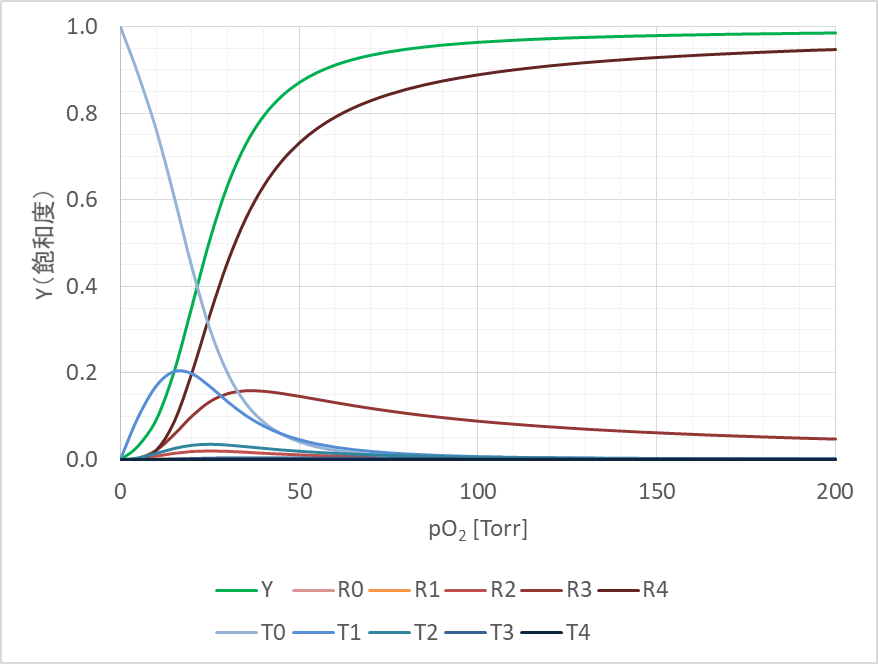
今回はアロステリック酵素の化学速度論に関するモデルについて紹介してみました。アロステリック酵素は以前に紹介したように代謝経路の調節のカギとなる場合が多い酵素です。その反応速度を理解することは代謝経路の全体の速度を理解することにもつながります。Michaelis Menten の式と異なり、少し複雑なモデルですが、数式を理解するいい練習にもなると思いますので、ぜひ本記事を参考に理解することにトライしてみてください。
参考文献
- 島原健三 (1991). 概説 生物化学. 三共出版. pp. 92-122
- Jeremy M. Berg, John L. Tymoczko, Gregory J. Gatto Jr., Lubert Stryer著、入村達郎、岡山博人、清水孝雄、中野徹訳 (2018). ストライヤー生化学 第8版. 東京化学同人. pp.198-262
- Donald V., Judith V., Charlotte P.著、田宮信雄、八木達彦、遠藤斗志也、吉久徹訳 (2017). ヴォート 基礎生化学 第5版. 東京化学同人. pp. 242-264
- Raymond Chang 著、岩澤康裕・北川禎三・濱口宏夫約訳 (2003) . 化学・生命科学系のための物理化学. 東京化学同人. pp.324 – 356