今回はアミノ酸配列を使って遺伝子間の進化的距離を算出してみましょう。実は塩基配列を用いた方が用いるモデルが複雑になります。これは塩基配列の方がコドン上の位置であったり、置換の組み合わせなど考慮する事項が多いためです。ですので今回はより簡単なアミノ酸配列の進化距離を測る数理モデルを紹介してみます。
ところで、アミノ酸配列を進化研究で使うにはどんなメリットがあるのでしょうか?アミノ酸は3塩基でコードされています。3塩基で表現できるコドンのパターンは 43=64 通りですが、アミノ酸は 20 種類しかありません。この差は異なるコドンが同じアミノ酸をコードすることを意味します。このため一見、塩基配列の方が情報を多く持っているように思われます。ですが、遠縁の配列を比較する場合はこの情報量があだになる場合が多いです。置換数が多すぎてうまく解析できないのです。こんな場合はアミノ酸配列を用いると、アミノ酸配列の方が塩基配列よりもよく保存されているので、遠縁の配列を比較する場合はアミノ酸配列の方が有利な場合が多いです。
Contents
もっとも単純な進化距離モデル、p 距離(p-distance)
p 距離は比較したサイト数に対して異なるアミノ酸が占めるサイトの割合で表現されます。


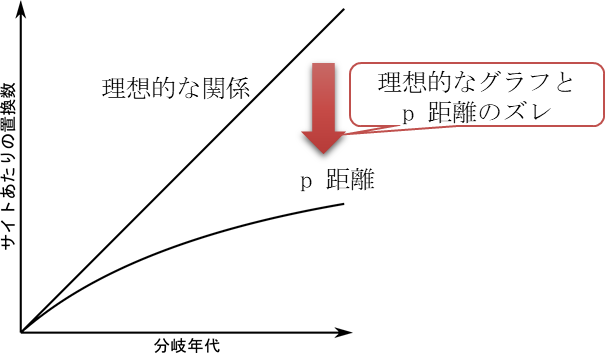
この距離は極めて簡単なモデルですが、遠縁の配列を比較した場合にはズレが生じます。このズレについて説明します。サイトあたりの置換数は基本的にランダムに起こるので分岐年代が長くなればなるほどサイトあたりの置換数は多くなります。ですので、サイトあたりの置換数を縦軸に分岐年代を横軸にとってグラフを作ると理想的には比例のグラフになるはずです。ところが、p 距離では比例にはならず、分岐年代が大きくなればなるほどズレていきます(図2)。このズレが生じる要因は様々なものがあります。どの要因に注目して補正するかによってさまざまな数理モデルが提唱されています。以下の項目でこのうちのいくつかを紹介します。
多重置換が原因で発生するズレの補正はポアソン正規補正距離 (poisson correction distance; PC distance) で
遠縁の配列を比較した場合、一つのサイトで複数のアミノ酸置換が起こっている場合があります。このような配列同士を比較した場合、異なるアミノ酸で占められたサイト数よりも実際のアミノ酸置換数が多い場合があります。当然ですが、このような多重置換は(ただでさえなかなか起きない変異が二回も起きるのですから)めったに起きることではありませんので、このような影響は近縁な配列同士では無視できます。しかし、遠縁の配列同士ではこれら多重置換の影響が表れてしまいます。これを補正するのがポアソン正規補正距離 (poisson correction distance; PC distance) です。算出方法は以下の通りです。
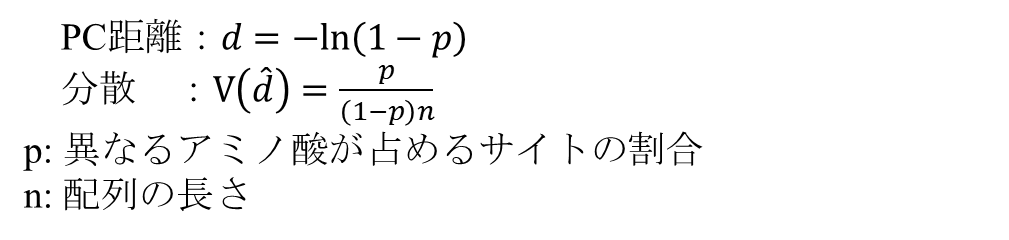
難しい計算は別の機会にして、ここでは概要だけ説明します。そもそもポアソン正規補正の名前にもなっているポアソン分布とは何でしょうか?ポアソン分布とは珍しい出来事(例えばとある場所で一定期間内に発生する事故件数のようなものです)を考える際に用いる分布です。あるサイトで置換が起きるというのは珍しい出来事になります。ですのでポアソン分布を使ってそのサイトに置換が起きる確率を推定するわけです。
数理モデルを考える際には前提条件を確認することがとても大切です。このモデルではすべてのアミノ酸サイトで置換速度が同じということを前提としています。つまり、配列のどこをとってもアミノ酸置換の起きやすさは同じであるということです。
サイトごとの置換速度に差がある場合はガンマ補正距離 (gamma distance)
機能的に重要な配列(機能を発揮する個所にかかわるアミノ酸とか、立体構造上重要なアミノ酸など)は一般にあまり変化しません。このような重要なアミノ酸が置換してしまうと機能に変化をもたらしてしまうため、不利な変異になる確率が高いからです。一方で機能的に対して重要でないアミノ酸置換速度が速くなる傾向があります。このようにサイトごとに置換速度が異なるような配列を扱う場合は、p 距離やポアソン正規距離のような置換速度を一定としたモデルでは扱えません。そこで用いるのがガンマ分布です。ここでは置換速度がガンマ分布に従うと仮定しています。この想定の基、計算することで以下のようなガンマ補正距離を算出することができます。

なお、上の数式で出てくる a はガンマ・パラメーター (gamma parameter) と呼ばれている数値で、分布の形を決定づけるパラメーターです。この数値により r の分布はいろいろな形に変化します。このため、a の値によってガンマ補正距離の計算結果は大きく影響を受けます。なお、p>0.2 かつ a<0.65 の時に r の影響が大きくなるため、p<0.2 で a>0.65 なら dG を使わなくても構いません。
アミノ酸の組み合わせで発生する置換速度の差がある場合に対応したモデル、Grishin の距離
アミノ酸には様々な特性があります。疎水性、塩基性、酸性などです。これらの特性が近いもの同士は置換しやすいという性質があります。このように置換するアミノ酸の組み合わせによっても置換速度が変動します。このような場合アミノ酸置換数を以下の数式によって推定することができます。

経験的に求めた置換頻度を使ったモデル、Dayhoff の距離
Dayhoff らは近縁なアミノ酸配列からアミノ酸の間で起きる置換の相対頻度を算出しました。この頻度をまとめたものをアミノ酸置換行列といいます。このアミノ酸置換行列を使ってアミノ酸置換数を推定するのが Dayhoff の距離です。なお、Dayhoff の距離は以下のように a=2.25 とした場合のガンマ補正距離でも近似できます。
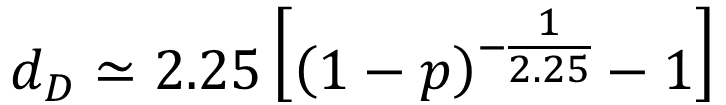
なお、Dayhoff と同様に経験的に求めた置換頻度を基にしているモデルに JTT (Jones-Taylor-Thornton) モデルというものがあります。 Dayhoff と同様にして求められたモデルですが、用いた遺伝子とその数が違っています。
今回はアミノ酸配列から進化距離を推定する数理モデルを紹介してきました。若干数学チックな内容も含んでいるのでとっつきにくいのですが、利用する上で重要なのは各数理モデルが前提としている条件と何に注目して設計されているモデルなのかという点です。まずはその点に注目して各手法を勉強してみてください。それでも余裕のある方は導出方法なども勉強してみると面白いので勉強してみてくださいね。