以前の記事で、系統樹解析の手順を概説しました。今回はこのうちアライメントについて記載しようと思います。簡単なアルゴリズムも併せてご紹介しますのでぜひ読んでみてください。
まずは 2 配列のアライメント (Alignment) で
例題としてアミノ酸配列 “GQKTCP” と “KQTLP” について考えてみようと思います。図のように縦横にそれぞれの配列を記載します。左上の赤丸から右下の赤丸(空)に至る経路を考えましょう。この経路がそれぞれの配列の並べ方を表します。まずは左上の赤丸から次のポイントに移動する場合を考えます。横向きのピンクの矢印を通る経路を考えた場合縦の配列の対応個所にギャップが入る経路です。一方で、縦方向のピンク矢印を通る経路では横の配列の対応個所にギャップが入ります。斜めの経路には二通りあって、オレンジの経路はアミノ酸が異なる経路で、青の経路ではアミノ酸が一致する経路です。これを左から右か、上から下方向に経路を選んでいくことですべての場合を考えることができます。この際、通った経路で要素が一致する経路 (α)、要素が一致しない経路 (β)、ギャップが入る経路 (γ) を数えておきます。こうして得られたα、β、γをもとに、以下の E を算出します。
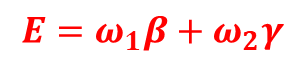
この数式では要素が一致しない経路の数とギャップが入る経路に重みを付けています。さて、今回の比較では極力両方の要素を一致させたいのでした。逆に言うと、要素が異なる場合やギャップが入る場合は極力避けて配列したいということになります。そこで上の式では β(要素が一致しない経路)と γ(ギャップが入る経路)を足し合わせた数値を計算しています。つまり、E とは不一致の度合いを表しているというわけです。ただし、置換が起こるメカニズムや頻度とギャップ(挿入)が入るメカニズムや頻度は異なるので、両者を同様には数えられません。そこでそれぞれの発生頻度に従って重みづけをしています(ギャップが入る頻度が置換が起こる頻度より低い場合、不一致度に与える影響はギャップの方が大きくなるので、ω1 はより小さく、ω2 はより大きく設定します。このようにして重要度の異なる変数を重要度に従って調整する操作のことを重みづけといいます)。さて、上述したようにこの E は不一致の度合いを表しているので、当然 E を最小にするように経路を決めていきます。そこで、いろいろな経路を考えて、最終的に E が最小になる経路を見つけます。一見大変そうですが、実際にはコンピューターに計算してもらえますのでご安心を。例えば、ω1=1、ω2=4 とした場合、図の左側のように経路をとると E=1×2+4×1=6 となり、最小になります。そしてこの経路が示すアライメント結果は縦配列のQとTの間にギャップが入った配置になります。
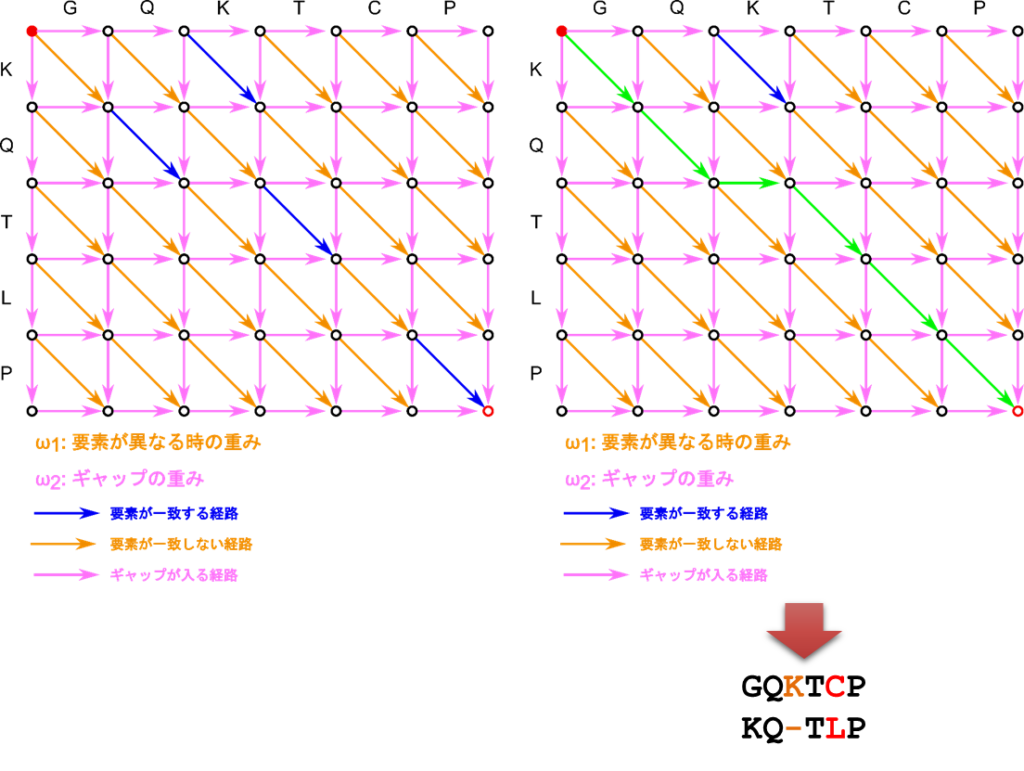
3配列以上のある場合のアライメントはどう処理するか?
マルチプルアライメント (multiple alignment) について記載します。この方法論は累進アライメント・アルゴリズム (progressive alignment algorithm) と呼ばれるアルゴリズムです。ベースは上記のアライメント手順がベースとなって、以下の手順で進めていきます。
①まずは距離の近いもの同士でアライメントを実行します。
②アライメント済みのものをグループ化します。
このグループ化というのはできたアライメントをギャップも含めて一つの配列のようにとらえなおすという意味です。この場合グループに属する配列がすべてひとまとめで扱われます。つまり、どこかにギャップが挿入された場合、グループに属する配列がすべてにギャップが入ります。
③より遠縁なグループ(配列)とアライメントを実行していきます。
①②を繰り返すことで順次遠縁のものともアライメント作成して、最終的な結果を得ます。
今回からは少し本格的な解析手法について紹介しています。アライメントの作成方法はまるでパズルのようで少し面白いですよね。今回は少し短いですがここまでにしようと思います。それでは最後まで読んでいただいてありがとうございました。