試験設計をする際に一試験群にどれくらいの n 数を割り付けるのかを悩んだことはないでしょうか?結局、カンで決定してみたり、慣習的に決定したり…なんてことも多いのではないでしょうか?実は試験群に割り付ける n 数の決定方法はきちんとしたやり方があります。今回はこのやり方について概要を説明しようと思います。
Contents
データをとるということは母集団からデータを抽出することに相当する
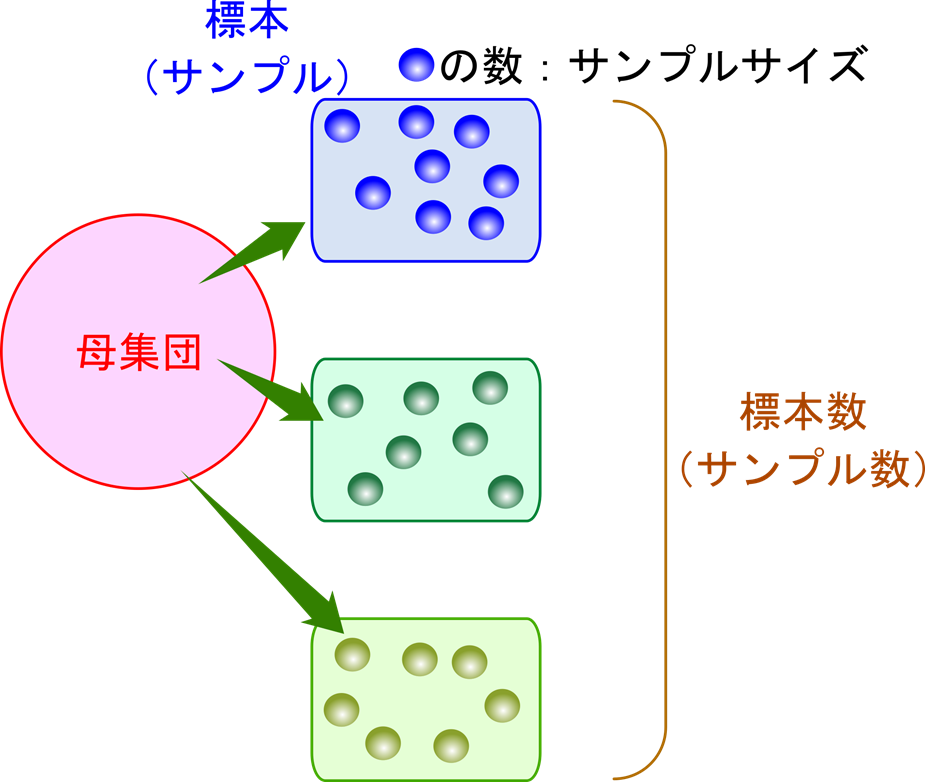
実験でデータをとるということはどういう意味を持つのでしょうか?ある実験を無限回数繰り返した時のデータの集団を母集団といいます。当然無限回数繰り返すなんてことは不可能です。母集団とは仮想の集団です。試験を実施してデータをとるということは母集団の中からデータを抜き出す行為に相当します。この操作を抽出、抜き出したデータの集まりのことを標本(サンプル)といいます。標本を形成するデータの数のことをサンプルサイズといいます。この辺りのイメージを図1に示しています。参考にしてくださいね。ここで注意です。統計学では今話している内容が母集団のことか標本のことかをきちんと区別をして下さい。例えば平均であっても母集団の平均か、標本の平均かによって全く意味が異なります。次に、サンプル数とサンプルサイズを混同する人がたまにいます。サンプル数とは標本の数のことを言います。標本に含まれるデータの数のことをサンプルサイズといいます。例えば試験を実施した場合の試験群の数をサンプル数、試験群を構成するデータの数(n 数とも言いますね)をサンプルサイズといいますので混同しないように注意してください。
二つの誤りと検出力
あるコインがイカサマコインかどうかが問題になったとします。表と裏が出る確率がそれぞれ 0.5 ずつであれば正しいコインと呼べますね。統計学ではこのような議論を行う場合、正しいコインであるということを一端認めます。そのうえで計算をしてみて、この仮説が成り立つ確率を算出してこの確率が一定以下であればいったん認めた仮説を否定するという手順をとります。なお、この否定することを棄却する、仮説を採用することを採択するといいます。さて、表の出る確率を P とすると
帰無仮説 H0:正しいコインである(P = 0.5)
対立仮説 H1:イカサマコインである(P ≠ 0.5)
とします。この時、最終的に否定したい仮説を無に帰する仮説ということで帰無仮説 H0、帰無仮説に対立する仮説を対立仮説 H1 といいます。
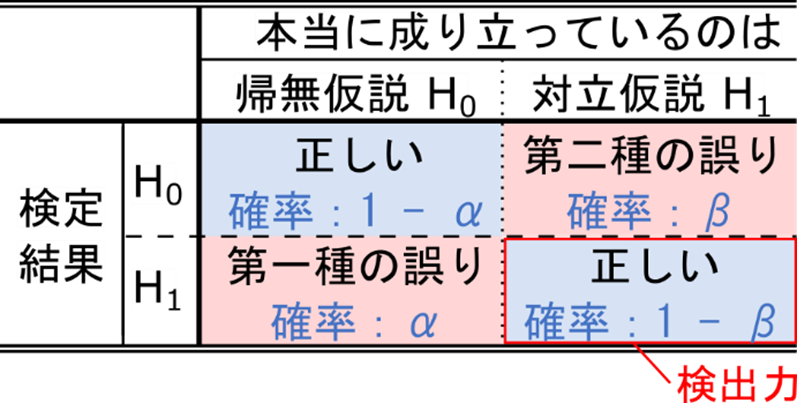
今、実際には H0 が成立するとしましょう。この時に検定を行った結果が H0 となった場合はこの検定は正しいといえますね。一方で H1 という結果が出ると間違っています。この場合に H1 を採択するという誤りは、本来コインが正しい(H0 が成立している)にもかかわらずイカサマコイン(H0 を棄却してします)と判断してしまうという誤りです。このような誤りのことを第一種の誤りといいます。第一種の誤りを犯す確率を α で表現します。この場合、正しい判断を下す確率は 1 – α ですね。次に、実際には H1 が成立するとしましょう。この時に検定結果が H0 となると誤ってしまいますね。この誤りは本来イカサマコイン(H1 が成立している)なのにもかかわらず正しいコイン(H0 を採択する)と判断してしまうという誤りです。このような誤りを第二種の誤りといいます。第二種の誤りを犯す確率を β で表現します。この場合、正しい判断を下す確率は 1 – β です。
ここで、本当は H1 が成立する場合にこれを正しく検出できる確率を検出力(power)といいます。先ほどそれぞれの仮説を
帰無仮説 H0:正しいコインである(P = 0.5)
対立仮説 H1:イカサマコインである(P ≠ 0.5)
と設定しましたね。H1 を正しく検出できる確率ということはイカサマコインを正しく見抜くことができる確率ということです。そう考えると検出力という呼び方は納得できるのではないでしょうか?
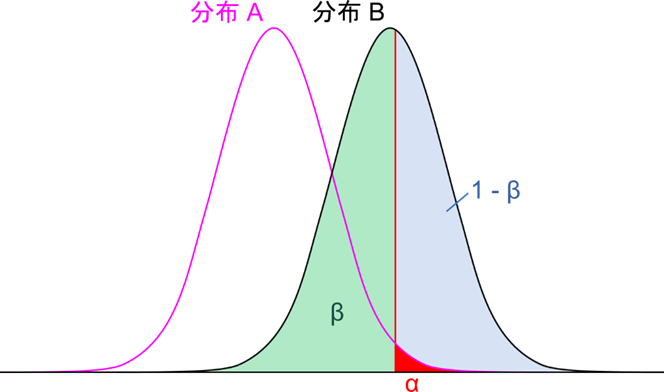
検出力はよく図2のような表現をされる場合もあります。これについても解説します。まず、検出力を考える場合には H1 が前提となるので分布が二つ存在する前提となります。今、分布 A について H1 を採択する場合を考えましょう。実際に観測された統計量よりも極端な統計量が得られる確率の合計のことを p 値といいます。この p 値が一定値(優位水準)より小さい場合に有意差があるとしてH0 を棄却して H1 を採択します。ところで優位水準とはある点より外側の部分の出現頻度を合計した値が一定値となる点のことです(図2の赤領域の合計)。つまり、観測された統計量が赤のラインより外側にあると有意差ありとみなされます。もう一方の分布 B から得られた統計量が赤のラインより内側にあると H0 は保留されますので、差があるとは言えないとなって間違ってしまいます。これが図2の緑の領域です。したがって、β は緑の領域の合計ということになります。一方で赤のラインより外側にある領域(図2の青の領域)は正しく差を検出できる領域ということになります。したがって検出力 1 – β は青の領域の合計ということになります。
二種の誤りの表では確率の合計が 1 にならない?
二種の誤りを説明した表で全部の場合を足したら 2 になるけど…?と疑問に思うかもしれません。実は今回扱っている問題は条件付確率に関する問題です。この確率はある条件の下で起こる確率を考えるものです。今の例では前提となる条件は「本当に成り立っているのは H0 である」ということです。この前提の下で検定結果は H0 か H1 かいずれしかないので検定結果が H0、H1 になる確率はそれぞれ α、1 – α となります。もちろん本当に成り立っているのが H1 の時も同様に考えて、検定結果が H0、H1 の確率はそれぞれ β、1 – β となります。言い換えると、本当に成り立っているのが H0 である場合、「本当に成り立っているのが H1 である」ことはあり得ないですね。ですので「本当に成り立っているのが H1 である場合」は一切考慮する必要がないということです。当然、本当に成り立っているのが H1 である場合でも「本当に成り立っているのが H0 である場合」はあり得ないので一切考慮する必要がありません。このように、最初の条件によって考える確率が変わるような問題を条件付確率といいます。ちなみに例えば A という条件の下で B が起こる確率を数式で Pr(B|A) と表します。統計学の本ではたまに出てくる表現ですので覚えておいてくださいね。
サンプルサイズは分布の形状に影響する
今、ある母集団から標本を抽出して統計量(平均など)を計算するという作業を無限に繰り返して、この統計量の分布をとることにします。様々な検定で使用される分布はこのような分布が利用されます。さて、この時、抽出するサンプルサイズをいろいろと変えてみます。すると図3に示すようにサンプルサイズが大きいと分布が細まり、サンプルサイズが小さいと分布の幅が太くなります。ですので実は検定というのはサンプルサイズを大きくすると有意差が容易に出てしまうという特徴があります。一方でサンプルサイズが小さいと有意差が出にくくなります。このため、適正なサンプルサイズを設定するということは正しく検定を行う上で重要になります。

効果量によって分布の離れ方を評価できる
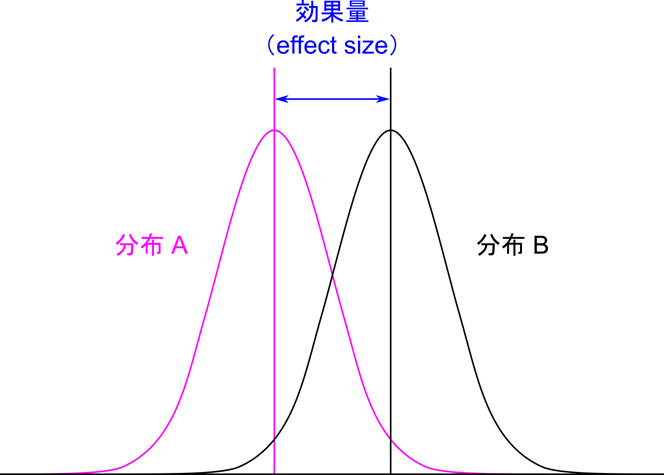
さて、このように分布の形がコロコロ変わる中で、有意差がある・ないという意味をどうとらえたらいいのでしょうか?この疑問を解決する上で重要な統計量に効果量(effect size)というものがあります。効果量というのは二つの母集団の代表値(例えば母平均など)の差をイメージするとよいと思います(具体的には標準偏差で標準化された数値です)。これまでの話ではサンプルサイズの差による分布の違いが影響して検定の結果が左右されてしまいます。そこで、互いの分布の距離も一緒に考えることでどれくらいの距離にあるときに有意差がどう判断されたのかという観点から評価することができるようになります。
優位水準、検出力、効果量を与えることで適正なサンプルサイズが決定できる
さて、長々と解説してきましたが、これでやっとサンプルサイズの話をする準備が整いました。いよいよサンプルサイズの設定について解説していきます。
サンプルサイズを設定することは正しく試験を評価するために極めて重要である
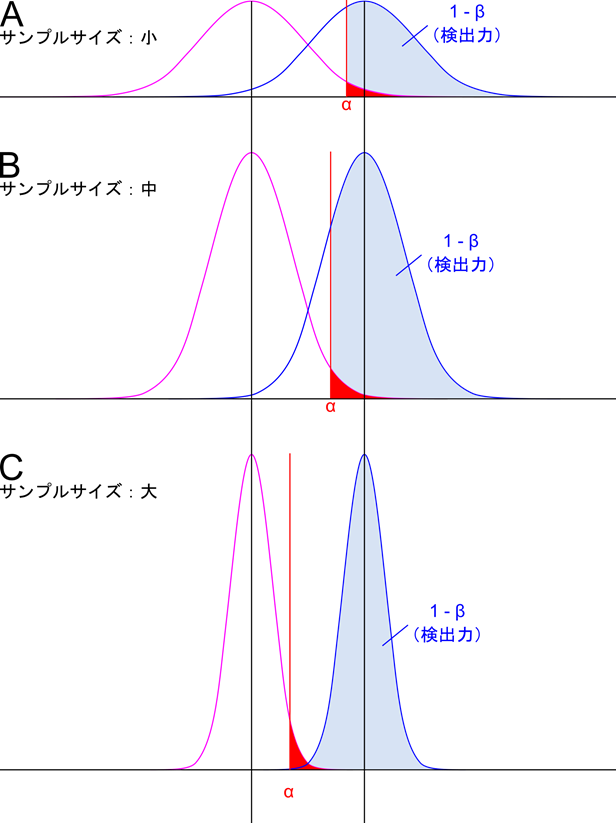
まずはサンプルサイズと有意差検定の関係を見てみましょう。図5は二つの分布の関係をサンプルサイズ別に並べて示しています。A ではサンプルサイズが小さいため分布は幅広くなっています。このため検出力(青の領域が占める割合)は小さくなっています。B ではサンプルサイズが中くらいに設定しています。すると検出力は少し大きくなります。C ではさらにサンプルサイズを大きくした場合で、検出力はかなり大きくなっていることがわかるかと思います。このようにサンプルサイズが変わると検出力も変わってきます。このことは二つの分布から抽出した標本が異なる母分散に由来すると判断される確率が変動することを意味します。検出力はA<B<C の順に大きくなっていくので、A よりも B が、B よりも C の方が有意差を出しやすいということになります。このことから、ただ単に有意差を出したいというだけならばサンプルサイズを大きくすればよいということになります。
ところが、これでは困ってしまう場合があります。例えば何も投薬していない群とあるワクチンを投薬した群で効果の有無を調べた場合を考えてみましょう。帰無仮説と対立仮説は
H0:無投与群とワクチン投与群の発症率が同じ
H1:無投与群よりワクチン投与群の発症率の方が小さい
と設定できます。さて、この場合に無投与群で発症率が 40 % なのに対して、ワクチン投与群では 35 % だった場合、本当にワクチン投与群の方がいいのか判断できませんよね(少なくともこのようなワクチンを投与すべきかは疑問です)。でも、サンプルサイズをあまりに大きくしてしまうとこの程度の差であっても有意差が出てしまうことになるわけです。一方で、無投与群の発症率が 40 % の時に、ワクチン投与群では 15 % 程度まで発症率が低下するならば、それなりに自信をもって有効だと判断できそうです。本来ならば後者のようなある程度自信をもって有効だと判断できるような場合でだけ有意性を検出できるように判定したいものです。ですので、試験する際には適正なサンプルサイズを設定することが重要ということになります。
サンプルサイズの設定方法(試験前の試験設計)
では、サンプルサイズの設定方法について説明します。ここでは試験を実施する前にサンプルサイズを設定する方法について解説します。このような解析手段を priori 解析といいます。
サンプルサイズを設定する上で必要となるのは優位水準、検出力、効果量を設定することです。優位水準は一般に 0.05 とすることが多いです。検出力は 0.80 とすることが多いです(Cohen によって提唱された数値です。興味のある方は参考文献に該当する本を載せていますので読んでみてください)。
一方で効果量は想定される数値を基に算出します。さて、ここで想定される数値ってどうやって考えるの?と聞かれそうですね。一つは事前に実施している試験の中から適正と思われる数値を設定するということが一つの方法になります。試験というのは単回で終わるということはあまりありません。似たような試験を何回も行うものです。ですので、事前に実施している類似した試験結果を基に数値を設定するのが一つの方法です。一方で先ほどのワクチンの例のように評価するにあたってこれくらいは満たしておいてほしいという想定がある場合があります。この想定を基に数値を設定するという方法がもう一つの方法です。いずれにしてもこれらの想定された数値を基に効果量が算出されます。効果量の算出方法は対象とする検定方法によってさまざまな計算方法がありますので、興味ある方は調べてみてください(参考文献の永田先生の書籍には各種の検定に対応する計算方法が詳述されています。少し難しいですがいい勉強になるので興味のある方はぜひ読んでみてください)。
こうして必要な数値が出そろいましたので、これらの数値を基にサンプルサイズを計算します。サンプルサイズの算出方法も検定方法によってさまざまな計算方法がありますが、非常に難しくなりますのでここでは割愛します。
これらの計算には自分で計算するのもいいですが、のちに紹介するプログラムを使用するのも一つの手段です。
検出力の検討(試験後の検証)
先ほどは priori 解析で試験設計をするための分析手段を紹介しました。一方で、試験後とった統計手段が適正であるのかを検討する場合もあります。このような解析手段は post hoc 解析といいます。
post hoc 解析では当然ながらサンプルサイズは試験したサンプルサイズで決まっていますね。優位水準はよくある数値として 0.05 とするのが一般的です。効果量は取得した試験結果から計算されます。これらの数値を基に検出力を算出します。つまり、post hoc 解析では実施した試験が適正な検出力で行われたのかを検証する目的で検出力を算出することになります。その結果、検出力が高すぎたり低すぎたりした場合、次回はサンプルサイズを考慮する必要があるということになりますね。
算出するために使用するのに有用なプログラム
最後に、効果量の算出やサンプルサイズの計算に有用なプログラムを紹介します。G-power というプログラムが開発されて公開されています。このプログラムはハインリッヒ・ハイネ大学デュッセルドルフ校の実験心理学研究所のホームページ(https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower.html)で公開されています。このプログラムでは代表的な検定方法に対応した priori 解析や post hoc 解析などが含まれています。ぜひ活用してみてください。
参考文献
- 永田 靖 著 (2003). サンプルサイズの決め方. 朝倉書店
- Jacob Cohen 著 (1988). STATISTICAL POWER ANALYSIS for the BEHAVIORAL SCIENCES Second Edition. Lawrence Erlbaum Associates.
- Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). GPower 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175–191. https://doi.org/10.3758/BF03193146
- Erdfelder, E., FAul, F., Buchner, A., & Lang, A. G. (2009). Statistical power analyses using GPower 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41(4), 1149–1160. https://doi.org/10.3758/BRM.41.4.1149
- Heinrich-Heine-Universität Düsseldorf, Allgemeine Psychologie und Arbeitspsychologie, “G*power” (https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower.html)