Contents
遺伝子配列間の差異は進化情報の蓄積
図1に遺伝子の進化の過程を例示しています。緑の枠で囲った配列が現在の配列とします。この配列は分岐する前(あるいは分岐直後)はもともと同じ配列だったはずです。これらがそれぞれで変化を蓄積していきながら進化していき、現在の配列になっています。現在の配列で蓄積した置換数は 8 塩基です。
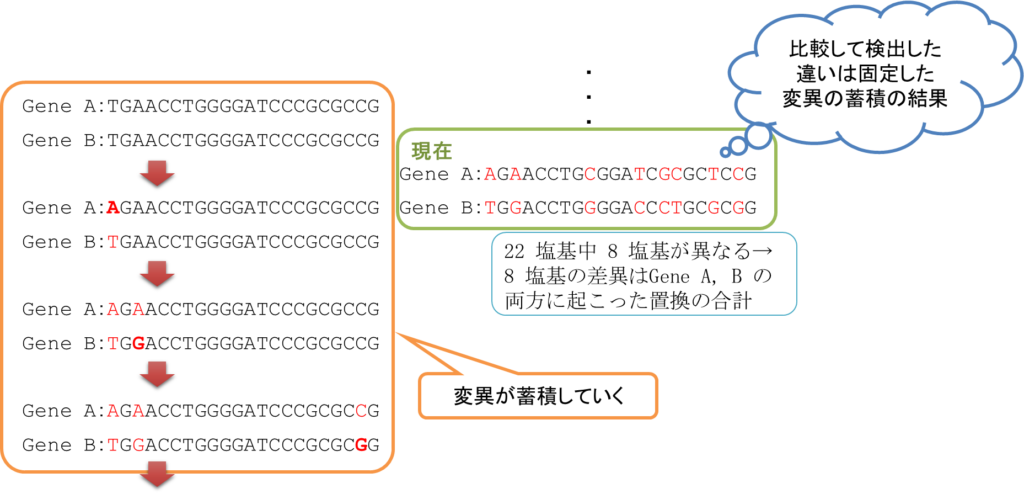
ところで、図1のように祖先の配列や祖先配列から現在の配列に至る途中の配列がわかっていることは(タイムマシンでもない限りは)まずありません。それでも現在の配列を比較することで、8 回の置換が発生していることだけはわかります。さらに、この置換がどちらの遺伝子で起こったものかはわかりませんが、両方合わせて 8 回ということはわかります。ですので、これら Gene A と Gene B の進化的距離を置換 8 回分の(あるいはこの数値から算出した)距離とみなすことができます。このように、現在の配列を比較することで祖先の配列を推定することはできませんが、比較した遺伝子の進化的な距離を測ることは可能です。
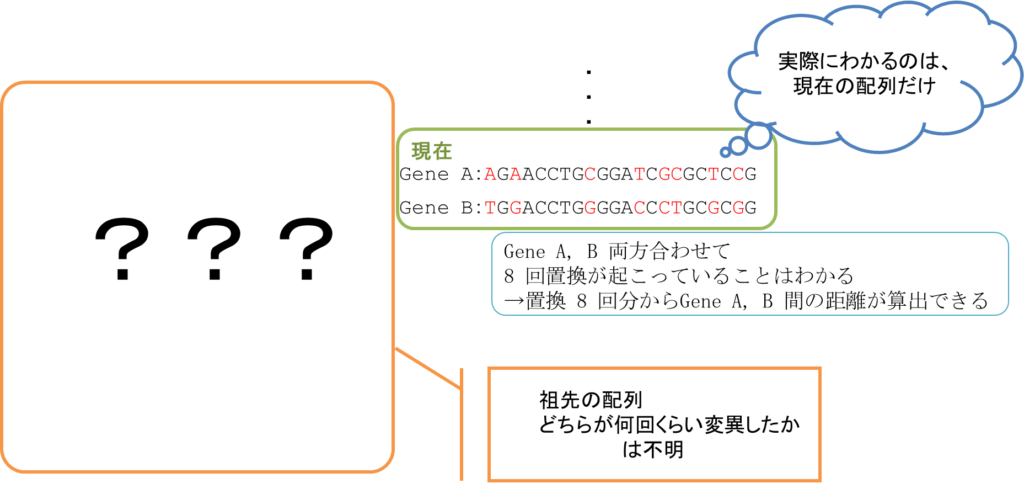
このように、遺伝子配列というのは進化の歴史の情報を刻み込まれた記録と見ることができるのです。
類似した遺伝子は共通の祖先を有する場合が多い
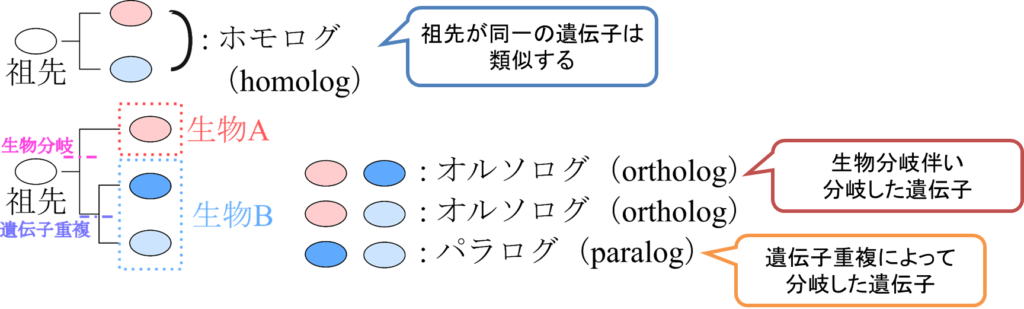
図1に示したように共通の祖先をもつ遺伝子は同一の配列がそれぞれの系統(祖先~子孫の関係にある一連のつながりと思っていただければいいかと思います。家系も系統の一例です)で変化が蓄積されていき、現在の姿になっています。このことから、同一の祖先をもつ遺伝子同士はもともと同一の祖先配列から変化していって現在の配列になっているので、ある程度類似することは容易に想像できるのではないでしょうか?このような関係にある遺伝子のペア(共通の祖先をもつ遺伝子のペア)のことをホモログ (homolog) といいます。ただし、ある程度類似した配列同士が真実、共通の祖先をもつのかといわれると実はわかりません。ですので、便宜上ある程度類似した配列同士のことをホモログと表現しています。
このような類似した遺伝子それぞれを別々の生物が有している場合、これらの遺伝子は生物の分岐に伴って分岐したと考えられます。このように、生物分岐に伴って分岐した遺伝子の関係を オルソログ(ortholog)といいます。例えば、ヒトの β-アクチンの遺伝子とマウスの β-アクチン遺伝子の関係がオルソログに相当します。
ところで、遺伝子とは元来変化してはならないものです(なんせ生物の設計そのものなのですから、遺伝子が変化してしまうということは設計が狂うことを意味します)。進化とは突然変異によって引き起こされますが、突然変異というのは極めてリスクの高い現象です。このようなリスクを避けつつ進化を実現するためにどうすればいいのでしょうか?生物はこの難題を遺伝子を増やすことで対応してきました。つまり、遺伝子を増やして互いに変化させることで、必要な遺伝子の機能が喪失するようなリスクを回避するわけです。このように遺伝子を増やす現象を遺伝子重複といいます。そして、遺伝子重複によってもホモログが出現します。このような関係にある遺伝子のペアをパラログ(paralog)といいます。
系統樹解析の手順の概略
系統樹解析を行うことで遺伝子配列から進化的な情報を読み取って解析することができます。ですので、系統樹解析を行うことを目的として、系統樹を作成するにあたって必要となる数理モデルやアルゴリズムを紹介していこうと思います。ただ、いきなり細かい話をしても混乱するだけだと思いますので、さしあたっては系統樹を作成する手順の概略を紹介しようと思います。
• 遺伝子配列の取得
データベースから取得する場合と、実際に配列を決定して取得場合があります。
データベースには Genbank(National Institute of health; NIH)、DDBJ(国立遺伝学研究所; NIG)、Embl-EBI(European Molecular Biology Laboratory; EMBL)の三つがあります。これらはデータベースに登録されている遺伝子配列は常に統合されているので、どのデータベースから配列を取得しても基本的に同じ情報を得られます。ただし、出力の様式が異なるので使いやすいデータベースを選択する方が良いと思います。
• アライメントを作成する

一致度が高くなるように配列を配置することをアライメントといいます。この点についてはまた詳細に紹介しようと思いますが、ここではごく簡単に触れておこうと思います。例えば図4のような配列があったとします。上側で比較してわかるように、前半は比較的一致しますが、後半が全く一致していませんね。そこで下側で行ったようにハイフン(赤字)を入れてあげることで後半もよく一致するようになります。これは Gene B のハイフンに相当する Gene A のサイトに配列 “G” が挿入されていることを意味します。このように配列をずらすことによって一致度が最も高くなるように配置しなおすことをアライメント (alignment) といいます。また、ハイフンのことをギャップ (gap) といいます。なお、今回は二配列だけで行いましたが、実際にはもっとたくさんの配列を使う場合がほとんどです。このように3配列以上を使ったアライメントをマルチプルアライメント(multiple (sequence) alignment)といいます。
• 適当な数理モデルで各配列間の距離を算出する
アライメント結果から、配列の違いから進化的な距離を計算します。この際に単純に異なる配列の割合とすることもあるのですが、シチュエーションによっては補正する必要があります。この補正方法に様々な数理モデルを使います。
• 算出された距離情報を基に系統樹を推定する
算出された進化距離を使って系統樹を作成します。この際の作成アルゴリズムには大きく分けて、距離法、最節約法、最尤法の三つがあります。また、それぞれの方法の中にもさらにいくつかの計算方法が提唱されています。
作成された系統樹の評価
系統樹解析は統計処理の一種です。ですので、たとえ一定の結果を得たとしてもきちんとした評価をしたうえで使用しなければなりません。このように系統樹の信頼性を評価する方法もいくつか考案されています。
今回は遺伝子配列を基にどうして進化の過程を推定できるのかという点について紹介してきました。また、遺伝子の分岐メカニズムの観点から遺伝子を分類してみました。さらに、系統樹解析の手順について概説もしました。今後はこれらの知見を基に、様々な数理モデルなどを紹介し行こうと思います。
最後まで読んでいただいてありがとうございました。